BAA013, BA008 Konstruktivní geometrie

BAA002, BA002 Matematika 2

- jaro 2020 -

Konzultační hodiny během zkouškového: pondělí 10:00 - 11:50 online zde , nebo po domluvě.
Email: mencakova.k@fce.vutbr.cz


Online cvičení:

BAA013 (BA008) Konstruktivní geometrie   -   materiály z videokonferencí

BAA002 (BA002) Matematika 2:  materiály z videokonferencí



Přihlášení:
- Přihlášení k online cvičení provedete nejlépe přihlášením k VUT Google účtu accounts.google.com/ ve tvaru ,,VUTlogin@vutbr.cz'' pomocí ,,vuthesla''. V seznamu aplikací (v pravo nahoře, symbol ,,3x3 tečky'') vyberete aplikaci ,,Kalendář'' a v ní by se Vám měla zobrazovat plánovaná online cvičení. Kliknutím na příslušný záznam v tomto kalendáři se Vám otevře webová stránka, kde pouze zmáčknete tlačítko ,,Připojit se" a měli byste být přihlášeni k videokonferenci.
- V případě, že se Vám nedaří přihlásit k VUT Google účtu, nevidíte žádné záznamy v Kalendáři nebo nechcete používat VUT účet, můžete se k online cvičení připojit kliknutím na příslušný odkaz na těchto stránkách. Pak se ke vstupu do videokonference použije účet, ke kterému jste zrovna přihlášeni v prohlížeči, nebo budete vyzváni, abyste se k nějakému účtu přihlásili.
- Pokud by webová stránka, na které má probíhat online cvičení nějak nefungovala, vyzkoušejte odkaz otevřít v jiném prohlížeči: doporučený je Google Chrome.
- Informace o VUT Google účtu, problém s heslem a podobně: http://apps.vutbr.cz/prihlaseni.
- V případě dalších dotazů napište na email: mencakova.k@fce.vutbr.cz.

________________________________________________________________________________


- Výuka podzim 2020 -



Podmínky k zápočtu:
- z jednoho zápočtového testu získat alespoň 10 bodů (maximum je 30 bodů). V případě dosažení 6-9 bodů, lze psát opravný test.


Online cvičení:

BAA001, BAA012 a BA001 Matematika 1   -   materiály z videokonferencí



BA003, BAA003 Matematika 3   -   materiály z videokonferencí



BA091 Základy deskriptivní geometrie   -   materiály z videokonferencí



________________________________________________________________________________



BA001 Matematika 1 a BA003 Matematika 3

- podzim 2019 -

Co_je_to Konzultační hodiny ve zkouškovém období: úterý 10:00 - 11:40, Z233
Email: mencakova.k@fce.vutbr.cz

Podmínky zápočtu:

BA001 Matematika 1


Příklady na procvičení: LU rozklad, 

Příklady probírané na cvičeních:

12. a 13. cvičení + analytická geometrie

DÚ (na 13. týden): Řeště soustavu rovnic:   -0,43 x1 -0,95 x2 +0,48 x3 = -7,34
1,28 x1 +5,58 x2 +3,25 x3 = 2,43
0,57 x1 -0,32 x2 -2,45 x3 = 2,15

11. cvičení

10. cvičení

Příklady k 2. zápočtovému testu, 

8. a 9. cvičení

  Taylorův polynom e^x (obrázek níže)

Tayloruv_polynom_exp(x)





































  Taylorův polynom sqrt(x+3) (obrázek níže)

Tayloruv_polynom_sqrt(x+3)



























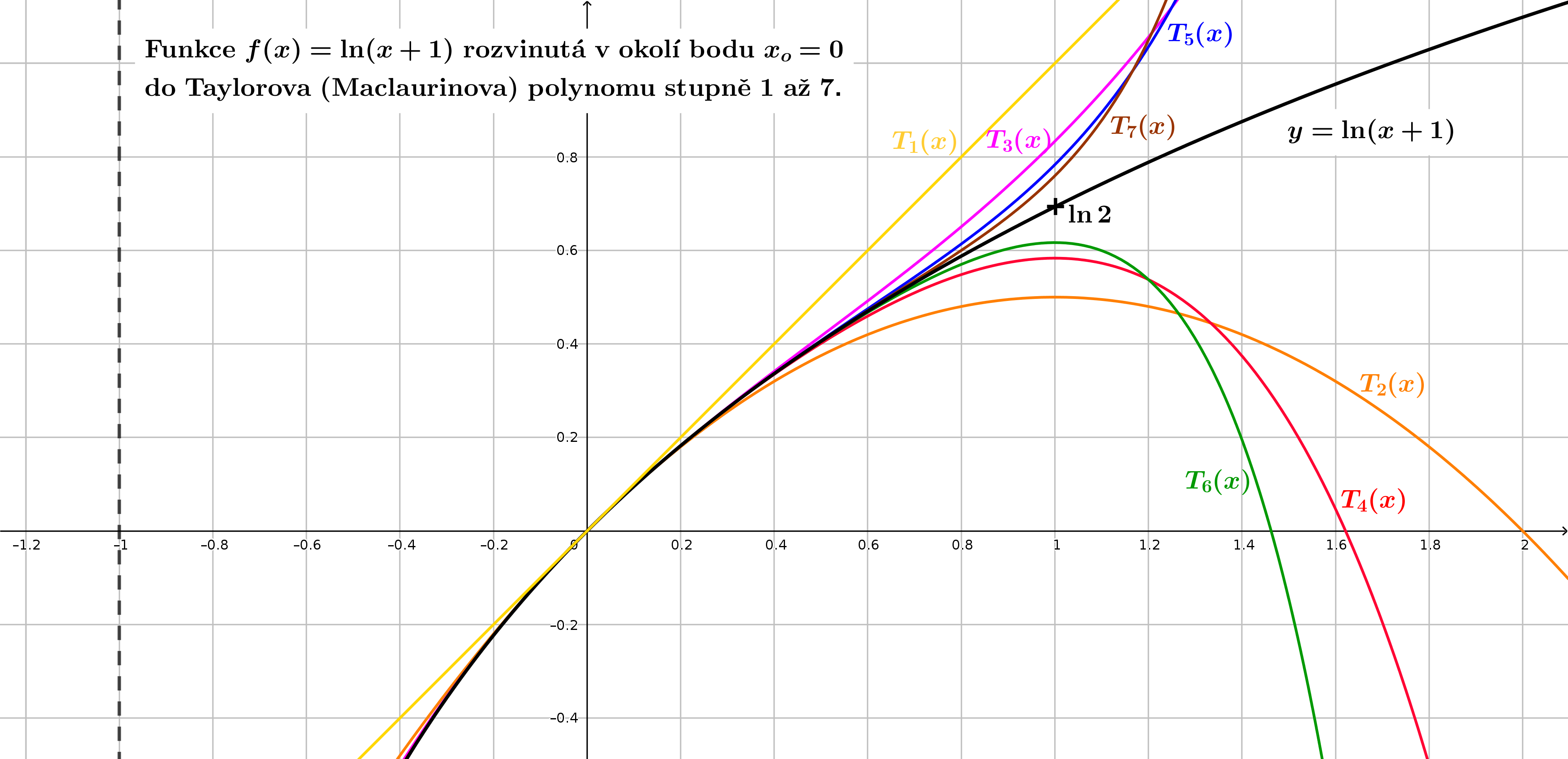
  Taylorův polynom ln(x+1) (obrázek níže)

Tayloruv_polynom_lnx+1 		ln 2 ≐ 0.6931471806
              chyba
 T1(x)=0.5   0.1931471806  
 T2(x)=0.83   0.1401861527
 T3(x)=0.583   0.1098138473
 T4(x)=0.783   0.0901861527
 T5(x)=0.616   0.0764805139
 T6(x)=0.7595238095   0.0663766289
 T7(x)=0.6345238095   0.0586233711
 T8(x)=0.7456349206   0.0524877400
 T9(x)=0.6456349206     0.0475122600
 T10(x)=0.7365440115   0.0433968309
 T11(x)=0.6532106782   0.0399365024
 T12(x)=0.7301337551   0.0369865745
 T13(x)=0.6587051837   0.0344419969
 T14(x)=0.7253718504   0.0322246698
 T15(x)=0.6628718504   0.0302753302
 T16(x)=0.7216953798   0.0285481992
 T17(x)=0.6661398242   0.0270073564
 T18(x)=0.7187714032   0.025624226
 T19(x)=0.6687714032   0.0243757774
 T20(x)=0.7163904508   0.0232432702
 T21(x)=0.6709359053   0.0222112753
 T22(x)=0.7144141662   0.0212669856
 T23(x)=0.6727474995   0.0203996811
 T24(x)=0.7127474995   0.0196003189
 T25(x)=0.6742859611   0.0188612195
 T26(x)=0.7113229981   0.0181758175
 T27(x)=0.6756087124   0.0175384682
 T28(x)=0.7100914710   0.0169442904
 T29(x)=0.6767581377   0.0163890429
 T30(x)=0.7090162022   0.0158690216
 T31(x)=0.6777662022   0.0153809784
 T32(x)=0.7080692325   0.0149220519
7. cvičení

6. cvičení

5. cvičení

4. cvičení +
DÚ: 1) Metodou R-F najděte přibližné řešení rovnice: 2x + sin x - 1 = 0, s chybou menší než ε=0,00001.
2) (cvičení pondělí a středa): Najděte interpolační polynom procházející body: [1; 0], [2; 3], [3; 2].
(cvičení čtvrtek od 10:00): Najděte interpolační polynom procházející body: [0; 3], [1; 0], [5; 2], [6; 6]. Ověřte polynom z hodiny.
(cvičení čtvrtek od 14:00): Metodou bisekce najděte přibližné řešení x2 rovnice: x4-x3+2x2-8 = 0, s chybou menší než ε=0,005.

3. cvičení + DÚ: Metodou bisekce najděte přibližné řešení x2 rovnice: x4-x3+2x2-8 = 0, s chybou menší než ε=0,005.

2. cvičení

1. cvičení + řešení



BA003 Matematika 3

> Pár příkladů na procvičení

Domácí úkol na 8. cvičení - pondělí 18.11.

Domácí úkol na 7. cvičení

> Pár příkladů na procvičení

Domácí úkol na 6. cvičení

Domácí úkol na 5. cvičení

Domácí úkol na 4. cvičení

Domácí úkol na 3. cvičení

Domácí úkol na 2. cvičení




MAPLE ( Úvod.pdf, Křivky - plot.pdf, 1. cvičení.mw)

Odkazy:

-------------------------------------------------------------------------------

BA008 Konstruktivní geometrie

- jaro 2019 -

Rysy:

             

Zadání úkolů:

2. týden Příklad 1. a 2. (Zadání si vytiskněte a dorýsujte nebo zadejte podobně.)

4. týden průnik hranolu/ jehlanu s přímkou.

Příklady, které budeme rýsovat na 8. cvičení: pracovní list 1, pracovní list 2.
Řešený příklad k samostudiu: průsečná metoda (zadání a řešení, prezentace).
9. týden Následující zadání si prosím přineste na příští cvičení. Při tisku dejte pozor na vytištění pdf dokumentu ve skutečném měřítku! stoupající cesta, napojení cest.
10. týden Příští týden (tj. 11. cvičení) budeme psát 2. zápočtový test (typové příklady níže; několik příkladů na procvičení zde).

11. týden Příklad 11. (PDF dokument se pokuste vytisknout ve skutečné velikosti.)

Řešení příkladů z 10. a 11. cvičení: vodorovná cesta, vodorovný oblouk, stoupající cesta.
12. a 13.
  týden 		Řešení příkladu na TP: napojení cest.

Teoretické řešení střech (příklady ze cvičení):
Obrázky ".png":
zakázaný kout 1, zakázaný kout 2, zakázaný kout 3, zakázaný kout 4, zakázaný kout 5,
zakázaný roh 1, zakázaný roh 2, zakázaný roh 3,
rovná střecha 6.
Stejné příklady jako ".html". (Obrázky lze otáčet - uchopte myší kdekoli na bílém pozadí v trojrozměrném modelu a pohybujte.):
zakázaný kout 1, zakázaný kout 2, zakázaný kout 3, zakázaný kout 4, zakázaný kout 5,
zakázaný roh 1, zakázaný roh 2, zakázaný roh 3,
rovná střecha 6.

Střechy - na procvičení

2. zápočtový test (typové příklady):

Kolmá axonometrie
- základní úlohy (sestrojení stopníků přímky, sestrojení stop roviny, průsečík přímky s rovinou, průsečnice rovin, rovina rovnoběžná s danou rovinou, ...),
- setrojení rovinného útvaru ležícího v některé z průměten,
- sestrojené tělesa s podstavou ležící v některé z průměten,
- průnik přímky s tělesem,
- řez tělesa rovinou.

Lineární perspektiva
- základní úlohy (nanesení výšky, sestrojení úsečky dané velikosti, sestrojení skutečné velikosti dané úsečky, sestrojení přímek pod daným úhlem, ...),
- sestrojení rovinného útvaru v základní rovině,
- sestrojení rovinného útvaru v rovině kolmé na základní rovinu,
- sestrojené tělesa s podstavou v základní rovině nebo rovině kolmé na základní rovinu.


             
6. týden Příklad 7.
V kolmé axonometrii ΔXYZ(55, 60, 55) zobrazte rotační kužel s podstavou k(S, r= 40 mm) ležící v půdorysně a výškou v= 80mm; S[60, 40, 0].

jaro 2017
             

Zadání úkolů:

Následující zadání si prosím přineste na 5. cvičení. Při tisku dejte pozor na vytištění pdf dokumentu ve skutečném měřítku! podélný profil.
Příští hodinu si prosím přineste čtverečkované papíry.

Odkazy: