Test č. 8

Deskriptivní geometrie, I. ročník kombinovaného studia FAST,
letní semestr 2000/2001

Šroubové plochy

První dva příklady jsou základní úlohy o šroubové ploše (podobné mohou být i na zápočtové písemce za letní semestr).

1. V Monge je dána "pravotočivá pravoúhlá uzavřená přímková šroubová plocha" osou šroubového pohybu o^p, o₁(0,30), parametr šroubového pohybu v_o=18, šroubuje se úsečka 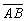, A[-50, 80, 25], B[-15, 45, 25]. Na ploše je dán bod T' jeho půdorysem T'₁[25, 42, ?]. Sestrojte jeho nárys T'₂ a odvoďte stopy p^t, n^t tečné roviny t.

   [výsledek přibližně: t(-250,5; 132; 77)]

2. V Monge je dána "levotočivá pravoúhlá otevřená přímková šroubová plocha" osou o šroubového pohybu, kolmou na p, o₁(0,40), parametrem pohybu v_o=20mm, šroubuje se úsečka 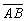, A[20, 60,30], B[70, 60, 30]. Na ploše je dán bod T' jeho nárysem T'₂[10, ?,46].

   1. Odvoďte půdorys T'₁ tohoto bodu.
   2. Sestrojte v bodě T' tečnou rovinu t plochy.

   [výsledek: stopy tečné roviny t(42,-42,17), y_T=80, přibližně.]

3. V kolmé axonometrii D(100,110,120) sestrojte jeden a čtvrt závitu "pravotočivé pravoúhlé uzavřené šroubové přímkové plochy", která je určena šroubováním úsečky 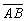. Šroubový pohyb je určen osou o=z a redukovanou výškou závitu v_o=15mm, A[40,0,0], B[0,0,0]. V bodě T[0,30,?] sestrojte tečnou rovinu t, včetně jejich tří stop p^t, n^t, m^t! Sestrojte křivku, která je čarou zdánlivého obrysu pro axonometrický průmět.

   [z výsledku: uvažujme tečnu g šroubovice plochy, tato šroubovice bodem T prochází a na ploše leží; potom půdorysný stopník P^g této tečny má být asi 2mm nalevo od průmětu osy z]
   Poznámka o umístění: přibližná poloha levého vrcholu X axonometrického trojúhelníka je od spodního okraje papíru A4 70 mm a od levého okraje papíru 50 mm.

4. V kolmé axonometrii D(100, 90, 80) sestrojte "pravotočivou kosoúhlou uzavřenou šroubovou přímkovou plochu", danou osou o=z šroubového pohybu, tvořící úsečkou 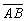, A[40.cos30^o;-40.sin30^o;0], B[0;0;20], skutečná velikost výšky závitu v=120. Sestrojte jednu výšku závitu i s vyznačením viditelnosti, zejména dbejte vyrýsování křivek axonometrického obrysu (tj. malých obloučků dole a nahoře nalevo), průmět šroubované úsečky se těchto křivek dotýká a od dotykového bodu mění svou viditelnost.

   Poznámka: rotační válec, nesoucí šroubovici bodu A má kruhovou podstavu se středem v počátku a poloměrem 40. Označme průsečík Q osy x (je nalevo) s kruhovou podstavou. Potom bod A je umístěn na této kruhové podstavě nalevo od bodu Q, pootočený od bodu Q o úhel 30^o ve smyslu otáčení hodinových ručiček.

5. V Mongeově projekci sestrojte "levotočivou cyklickou šroubovou plochu", jestliže rovina šroubované kružnice je svislá a prochází navíc osou o (označovanou v literatuře historickým jménem "Plocha sv. Jiljí" podle poprvé zaznamenaného stavebního uplatnění v jisté stavbě stejného názvu). Byla použita jako plocha nad šroubovým schodištěm, které propojuje dvě chodby s valenými klenbami, avšak chodby jsou v různých úrovních.
   V úloze je plocha určena levotočivou šroubovicí k, uplatněnou na střed S[-55,80,27], poloměr kružnice h o středu S je 27, osa šroubového pohybu o prochází bodem Q[0,80,0], o^p, výška řídicího kužele v_o=20mm. Šroubujte jenom horní polovinu kružnice h o polovinu výšky závitu nahoru. Bod S očíslujeme indexy jako 0, dále pak 1, 2, ... nahoru. Vyznačte viditelnost vzhledem k nárysu (dovnitř plochy bude částečně vidět).

   1. Sestrojte půdorysný obrys plochy.
   2. Sestrojte nárysný obrys plochy (s vyznačením i viditelných částí vnitřku klenby, tj. neviditelné části kružnic čárkovaně a viditelně plně).
   3. Sestrojte tečnou rovinu t, která se plochy dotýká v bodě T na kružnici ²h o středu v bodě 2 (tj. odkloněné od výchozí kružnice se středem S₁ o úhel 60^o.Bod T volte na této kružnici tak, aby vzdálenost bodu T od osy o šroubového pohybz byla asi 49mm.

   Pro konstrukci tečné roviny užijte tečny t šroubovice bodu T a ještě tečny g kružnice ²h, která má střed v bodě 2. Konstrukci tečné roviny t zakončete vyhledáním jejich stop p^t, n^t.

   [z výsledku: půdorysný stopník P^g by měl mít polohu asi 68mm od osy o, jeho nárys asi 49mm od osy o₂]

6. V Mongeově projekci sestrojte "Archimedovou serpentinu", která je určena: pravotočivou šroubovicí k=(o,v^o), kde osa o šroubovice k prochází bodem Q[0,80,0] kolmo k půdorysně (QÎo^p), redukovaná výška závitu (čili parametr šroubového pohybu či výška řídicího kužele) v_o=15mm, šroubuje se kulová plocha o středu S[0,110,0] (který bude ležet na dané šroubovici) a poloměru r=20mm.

   1. Sestrojte oba průměty plochy, tj. obrys plochy v nárysně a v půdorysně. Poznámka pro případnou pomoc ze strany třetí osoby při samostudiu: Pro nárys body vratu na čáře zdánlivého obrysu sestrojte jen přibližně. První průmět této čáry (skutečného obrysu vzhledem k nárysně) v půdorysu nemusíte sestrojovat.
      Čarou skutečného obrysu vzhledem k půdorysně je rovníková a hrdlová šroubovice. Sestrojte nárys těchto šroubovic, konstrukce je celkem snadná.
   2. plochu serpentiny ukončete dole kulovou plochou o středu S a nahoře ve výšce jednoho závitu tvořící kružnicí ¹²m (která je dotykovou kružnicí kulové plochy se serpentinou a jejím průmětem bude elipsa).
   3. sestrojte tečnou rovinu t, která se plochy dotýká v bodě T, včetně jejich stop p^t a n^t. Bod T leží na horní polovině tvořící kružnice ³m a má T[40,?,?]. Číslujeme od bodu S (číslo 0) vzestupně pravotočivě, v půdoryse proti směru pohybu hodinových ručiček (tj. souřadnice bodu ³S[30,80,?])

   Poznámka: pokud si vezmete na pomoc pro konstrukci tečné roviny t k tomu konstrukci tečny g, dotýkající se kružnice ³k v bodě T, můžete pro ni užít místní osové afinity mezi průmětem kružnice ³m, (kterým je elipsa) a afinním obrazem kružnice. Ten získáme, jestliže kružnici ³m na okamžik otočíme do vodorovné polohy.
   Lze však mnohem jednodušeji uvážit, že tečná rovina t je v prostoru kolmá k poloměru kulové plochy, směřujícímu ze středu kulové plochy k bodu T. (Poloměr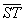 kulové plochy je ale velmi krátká úsečka a konstrukce bude proto zatížena jistou nepřesností.) Pro konstrukci roviny t, (kolmé k poloměru) bychom užili hlavních přímek obou osnov roviny t (vedených bodem T) a jejich kolmých průmětů k průmětu této úsečky, dále stopníků těchto hlavních přímek, atd. ...
   [přibližný výsledek pro stopy tečné roviny: t(150, ?, 100), dále y-ová souřadnice půdorysné stopy vychází příliš daleko, ale půdorysná stopa prochází např. stopníkem P^h hlavní přímky, P^h[93,85,37]=asi]

Odevzdávejte poštou a najednou všechny příklady. Budou Vám vrácené opravené poštou přes děkanát. Poznámka při opravách "znovu" znamená je přerýsovat.

Test č.8 odevzdejte do konce měsíce května 2001 .

RNDr.Pavel Talanda,v.r.

Aktualizace dne 04.06.2002
Copyright © Jan J. Šafařík