Předpokládejme, že funkce
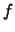 ,
,
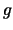 mají spojité druhé parciální
derivace a že jsou známé aproximace
mají spojité druhé parciální
derivace a že jsou známé aproximace
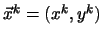 blízko přesného řešení
blízko přesného řešení
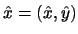 úlohy (11).
Aproximujeme-li nulové hodnoty
úlohy (11).
Aproximujeme-li nulové hodnoty
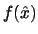 ,
,
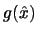 Taylorovým polynomem prvního stupně v okolí bodu
Taylorovým polynomem prvního stupně v okolí bodu
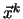 ,
vznikne
,
vznikne
|
|
(14) |
![]()
|
|
(15) |
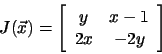
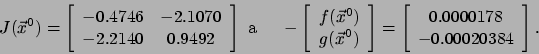
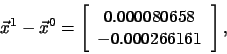
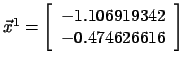 .
Stejným postupem byly vypočteny i aproximace
.
Stejným postupem byly vypočteny i aproximace
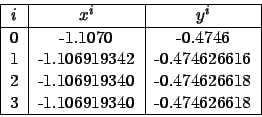
Up: Řešení systémů nelineárních rovnic
Previous: Metoda prosté iterace
Obsah