|
|
|
|
|
|
|
|
|
(12) |
Next: Newtonova metoda (metoda linearizace)
Up: Řešení systémů nelineárních rovnic
Previous: Řešení systémů nelineárních rovnic
Obsah
|
|
|
|
|
|
|
|
|
(12) |
![]()
![]()
![]()
zvolí se
![]() a výpočet se ukončí, jakmile
a výpočet se ukončí, jakmile
![]()
zvolí se
![]() a výpočet se ukončí, jakmile
a výpočet se ukončí, jakmile
![]() .
.
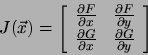
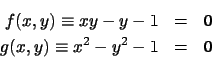
|
|
(13) |
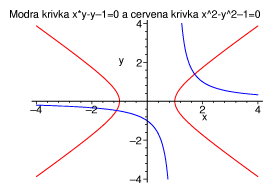
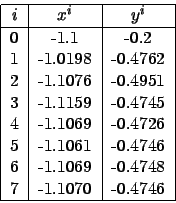
Obrázek 5
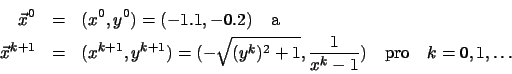
Next: Newtonova metoda (metoda linearizace)
Up: Řešení systémů nelineárních rovnic
Previous: Řešení systémů nelineárních rovnic
Obsah