hledá pro danou
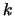 -tou aproximaci
-tou aproximaci
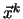 a pro
a pro
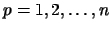
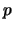 -tou souřadnici
-tou souřadnici
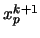
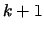 -té aproximace
-té aproximace
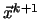 jako tu hodnotu
jako tu hodnotu
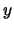 , pro niž je splněna rovnice
, pro niž je splněna rovnice
![]()
|
|
(7) |
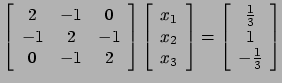 řešte Jacobiovou metodou: Z (7) plyne
řešte Jacobiovou metodou: Z (7) plyne
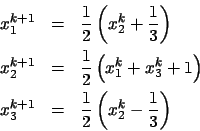
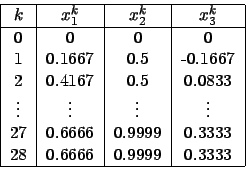
![]()

![]()

Next: Gaussova-Seidelova metoda
Up: Iterační metody řešení systémů
Previous: Iterační metody řešení systémů
Obsah