Konstrukce sítě, pláště kosého kruhového kužele,
specielně konstrukce bodů jeho rozvinuté kruhové hrany
Poznámky jsou použitelné v Testu č.6, LS 2000/2001
Jednotlivé body kruhové hrany jsou očíslovány a převáděny do sítě postupně, zcela samostatně.
Kosý kužel je nahražen dvanáctibokým jehlanem; čím více vrcholů podstavy jehlan bude mít, tím tato náhrada bude přesnější a tím přesnější bude i síť. Užijeme nejméně dvanácti vrcholů, jehlanu.
Kužel pomyslně rozstřihneme podél površky v jeho rovině souměrnosti, může to být površka (podle očíslování) 1V nebo 7V. Zvolíme 7V, naopak površka 1V bude v důsledku toho v síti uprostřed a proto ji umístíme na papír uprostřed, protože síť bude vznikat na obě strany.
| samostatné nákresy ke konstrukcím: | ||
|---|---|---|
| site_1.jpg (28 KB) | site_2.jpg (32 KB) | |
| text bez použití fázových obrázků: | ||
|---|---|---|
| site.html | ||
| Tento text si zde můžete stáhnout ve formátu .PDF a nebo .PS: | ||
|---|---|---|
| site.pdf (84 KB) | site.ps (104 KB) | |
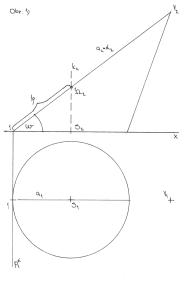
# OBR. 1 : Povrchová přímka se stopníkem 1
Povrchová přímka se stopníkem 1 je dotykovou přímkou tečné roviny a a protože površka je kolmá k půdorysné stopě pa , je také spádovou přímkou tečné roviny a.
# OBR. 2 : Površka se stopníkem číslo 7
Také tady je površka kolmá ke stopě pb, protože je v osovém řezu souměrnosti roviny SV kosého kužele
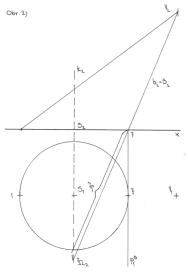
# Princip sítě (zatím bez oskulačních kružnic):
Pro síť musíme zjistit skutečnou délku každé obecné površky. To se dá udělat nejjednodušeji prostým jejím sklápěním do půdorysny. Délky obloučků na kruhové podstavě jsou všechny stejné a my je můžeme (s jistou nepřesností) nahradit jejich tětivami. Nyní postupně klademe vedle sebe boční stěny jehlanu (ten je náhradou za kužel). Narýsujeme si v síti první površku 1V (ve skutečné velikosti). Od vrcholu V na této površce v síti vynášíme kružítkem oblouček a v kružítku máme skutečnou délku další površky 2V. Z bodu 1 kružítkem vynášíme pak zase oblouček a v kružítku máme délku tětivy (jedné dvanáctiny), až se oba obloučky protnou. Průsečík těchto dvou obloučků je bod 2. Připravíme délku 3V, nachystáme pro 3V oblouček. Kružítkem budeme také dbát, aby délky tětiv 12, 23, atd. byly stále stejné. Nezapomeneme, že síť bude symetrická a proto vždy sestrojujeme body, vzájemně souměrné, jsou to např.:2a 12, dále 3 a 11, dále 4 a 10 atd.
# Obr.3.a) : Površka se stopníkem 3 je již obecná
V dalším budeme mít obecnou površku. Práce s touto površkou se dá aplikovat (když by bylo třeba, u nás nepožadujeme) na každou další obecnou površku. Nyní površka není spádovou přímkou (je zde odkloněna doprava od spádové přímky) a vrchol V tudíž už na spádové přímce neleží.
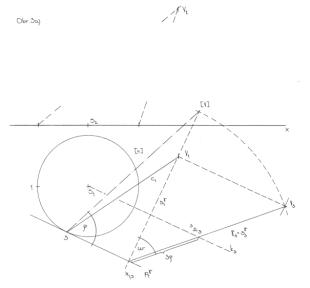
zavedeme středem S kolmici k. Poloměr oskulační kružnice je však i nyní třeba měřit na spádové přímce sg se stopníkem 3 (spádová přímka je ale vůči nárysně natočená, takže v náryse poloměr už nemůžeme změřit)
zavedeme proto novou, třetí průmětnu l, rovnoběžnou s poloměrem na spádové přímce sg (spádová přímka musí být kolmá ke stopě pg a proto i nová třetí průmětna l a osa x1,3 musí být kolmá k této stopě pg
novou průmětnu popíšeme pro sklápění jako osu x1,3, umístíme ji do volného místa napravo od kužele, celkem kamkoliv. Je zvykem zavést tuto osu sklápění přímo vrcholem V kužele
doprava a kolmo k ose sklápění sklopíme výšku vrcholu a označíme jako V3, stopník 3=P této površky převedeme do třetího průmětu jako P3. Spojením P3V3 získáme třetí průmět površky (tečná rovina g a její spádová přímka sg3 se také ve třetím průmětu promítá do této površky)
odvodíme třetí průmět k3 kolmice k, vedeme připraveným třetím průmětem S3. Průsečík 3W=k3 Çs g3, (tedy průsečík kolmice s tečnou rovinou) poloměr oskulační kružnice je pak vzdálenost P33W.
# Převedení do sítě :
 Především připravíme površku 3V. Koncepce:
nejdříve musíme v síti od površky 3V odklonit o úhel
j (o úhlu později) půdorysnou stopu tečné
roviny g. Tato stopa přechází v tečnu
rozvinuté kruhové hrany. Potom poloměr oskulační kružnice se bude vynášet k
této tečně kolmo, koncový bod 3W.
Do něj zabodneme kružítko a sestrojíme oskulační kružnici o poloměru
P3W3 z třetího
průmětu.
Především připravíme površku 3V. Koncepce:
nejdříve musíme v síti od površky 3V odklonit o úhel
j (o úhlu později) půdorysnou stopu tečné
roviny g. Tato stopa přechází v tečnu
rozvinuté kruhové hrany. Potom poloměr oskulační kružnice se bude vynášet k
této tečně kolmo, koncový bod 3W.
Do něj zabodneme kružítko a sestrojíme oskulační kružnici o poloměru
P3W3 z třetího
průmětu.
Nyní k úhlu j :
Jedná o skutečnou hodnotu úhlu mezi dotykovou površkou 3V a půdorysnou
stopou příslušné tečné roviny. Ten se zásadně do sítě vždy převádí z tečné
roviny ve skutečné velikosti (a každá tečná rovina postupně se sítí
splyne). Protože úhel j je v nakloněné
tečné rovině g, je v prvním průmětu
zkreslen, menší. Abychom zjistili jeho skutečnou velikost, musíme tečnou
rovinu g otočit do půdorysny kolem její
půdorysné stopy pg. Stačí, když
otočíme vrchol V. K tomu nám dobře poslouží zde již využitá třetí
průmětna. Poloměr je vzdálenost (měřená na třetím průmětu spádové přímky
sg3 od stopníku
P3 po vrchol V3). Vytvoříme kružítkem
oblouček otáčení bodu V do půdorysny. Na prodlouženém 1. průmětu
spádové přímky sg1
označíme kružítkem (otočený) bod [V]. První průmět površky
c1=PV1 přejde do otočené površky [c]=P[V],
čerchované. (Upozorňujeme na tomto místě, že otočená površka je zde ve skutečné
velikosti, takže její délku můžeme srovnat s délkou již dříve nalezenou
sklápěním. Vždy ale pro síť použijeme sklápění, případně ještě "další metodu",
protože je to rychlejší. Tou "další metodou" (někdy stručně zvanou "jeřábová")
rozumíme otáčení všech promítacích rovin,(rovin, kolmých k půdorysně) všech
površek do polohy rovnoběžných s nárysnou. To se dá udělat otáčením okolo
vertikální osy o, vedené společným bodem V všech površek. Takže
nyní již mámě otočenou površku [c]. Mezi touto otočenou površkou a
půdorysnou stopou je už hledaná skutečná velikost tohoto úhlu
j. Tento úhel
j kružítkem (zvolíme dva obloučky libovolných,
ale stejných poloměrů a přes obloučky ještě užijeme shodně velké tětivy)
přeneseme do sítě, obr.3b), a úhel vyneseme od površky 3V na správnou
stranu (podle postupně kladených površek kužele do sítě), nejspíše bod
2 bude od bodu 3 nalevo a bod 4 od bodu 3 zase
naopak napravo.
# Obr.4: Površka 4V, se stopníkem 4
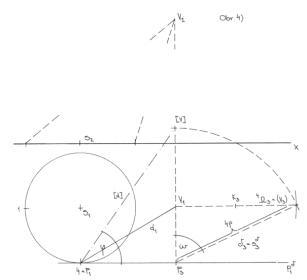 V principu se zde postup neliší od površky 3V, zase půjde o obecný bod
kruhové základny. Půdorysná stopa
pd1 je nyní specielně
rovnoběžná s S1V1 či s osou
x1,2. Zase užijeme pomocnou třetí průmětnu, stále ji budeme
pro srozumitelnost označovat jako třetí, kolmou k půdorysné stopě
pd1. Vedeme ji
(úspora místa) vrcholem V1. Sklopíme doprava vrchol
V1 do bodu V3. Stopník
4=P1 převedeme do P3. Pomocný třetí průmět
tečné roviny bude splývat s třetím průmětem spádové přímky
P3V3=sd3
=d3. Sestrojíme třetí průmět
kolmice S3V3=k3. (Vrchol V na
kolmici v prostoru neleží, je zcela mimo napravo). Ve třetím průmětu tentokráte
specielně je kolmice k3 s vrcholem V3 v
zákrytu . Také průsečík
4W3 bude v zákrytu s
vrcholem V3, tzn.
4W3=V3. Tudíž
poloměr 4r=P3
4W3.
V principu se zde postup neliší od površky 3V, zase půjde o obecný bod
kruhové základny. Půdorysná stopa
pd1 je nyní specielně
rovnoběžná s S1V1 či s osou
x1,2. Zase užijeme pomocnou třetí průmětnu, stále ji budeme
pro srozumitelnost označovat jako třetí, kolmou k půdorysné stopě
pd1. Vedeme ji
(úspora místa) vrcholem V1. Sklopíme doprava vrchol
V1 do bodu V3. Stopník
4=P1 převedeme do P3. Pomocný třetí průmět
tečné roviny bude splývat s třetím průmětem spádové přímky
P3V3=sd3
=d3. Sestrojíme třetí průmět
kolmice S3V3=k3. (Vrchol V na
kolmici v prostoru neleží, je zcela mimo napravo). Ve třetím průmětu tentokráte
specielně je kolmice k3 s vrcholem V3 v
zákrytu . Také průsečík
4W3 bude v zákrytu s
vrcholem V3, tzn.
4W3=V3. Tudíž
poloměr 4r=P3
4W3.
Skutečná velikost úhlu j:
Poloměr otočení bodu V okolo půdorysné stopy
pd1 měříme zase ve
třetím průmětu (jako vzdálenost bodů
P34W3, zde
specielně P3V3). Provedeme oblouček až nalezneme
na prodloužené spádové přímce
sd1 bod [V].
Tento bod spojíme se stopníkem P1 površky. Tak přejde
původní 1. průmět površky d1=P1V1 do
otočené površky [d]=P1[V]. Její odchylka od půdorysné stopy
pd1 je už skutečná
velikost úhlu j, použitelná pro síť. (V síti
zase vyhledáme površku 4V, kružítkem přeneseme tento úhel
j a toto nové rameno úhlu označíme jako tečnu
rozvinované kruhové hrany. Potom v bodě 4 této hrany sestrojíme kolmici
a na ni naneseme předem změřený poloměr
4r, koncový bod označíme v síti
jako 4W. Z tohoto středu sestrojíme
opět oskulační kružnici.)
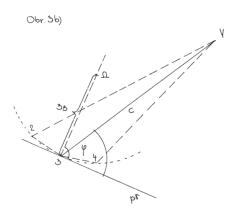
# Obr.5.: Inflexní bod J rozvinuté kruhové hrany
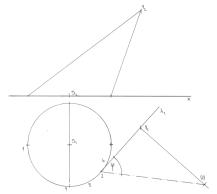 Má-li na okamžik přejít oskulační kružnice v inflexní tečnu=přímku, která
změní znaménko křivosti rozvinuté kruhové hrany v opačné, křivost bude tedy
opačná, obr.5b), musí mít tudíž v takovém okamžiku tato oskulační kružnice
nekonečně velký poloměr. Aby došlo k nekonečně velkému poloměru, potom
příslušný bod
JW tečné roviny "nesmí být po
ruce", musí naopak také být až v nekonečnu. Protože bod
W je však zásadně průsečík kolmice k s tečnou
rovinou, musí být nyní specielně tato kolmice k s tečnou rovinou přímo
spolu dokonce rovnoběžná. Protože však kolmice k od začátku tvorby
sítě zaujímá trvale kolmou polohu k rovině kruhové základny kužele, k
půdorysně (a prochází stále středem S), nezbývá než připustit, že i
tečná rovina musí být kolmá k půdorysně (aby si ponechala svoji rovnoběžnost
s uvedenou kolmicí).
Má-li na okamžik přejít oskulační kružnice v inflexní tečnu=přímku, která
změní znaménko křivosti rozvinuté kruhové hrany v opačné, křivost bude tedy
opačná, obr.5b), musí mít tudíž v takovém okamžiku tato oskulační kružnice
nekonečně velký poloměr. Aby došlo k nekonečně velkému poloměru, potom
příslušný bod
JW tečné roviny "nesmí být po
ruce", musí naopak také být až v nekonečnu. Protože bod
W je však zásadně průsečík kolmice k s tečnou
rovinou, musí být nyní specielně tato kolmice k s tečnou rovinou přímo
spolu dokonce rovnoběžná. Protože však kolmice k od začátku tvorby
sítě zaujímá trvale kolmou polohu k rovině kruhové základny kužele, k
půdorysně (a prochází stále středem S), nezbývá než připustit, že i
tečná rovina musí být kolmá k půdorysně (aby si ponechala svoji rovnoběžnost
s uvedenou kolmicí).
Hledáme tedy takovou površku JV, která svou tečnou rovinu bude mít
kolmou k půdorysně. Toto je možné jen pro případ, že površka JV je pro
pohled shora na půdorysnu právě obrysovou površkou. Abychom površku
získali, vedeme bodem V1 tečnu ke kruhové podstavě a
vyznačíme její dotykový bod J1 (na poloměru, kolmém k tečně).
Bod
J do sítě přeneseme interpolačně, tj. odhadneme jeho polohu na podstavě
(mezi body 5 a 6), tyto body už před tím budeme v síti mít a
potom mezi ně bod J umístíme. Připravíme v síti i površku JV.
Nyní musíme vyhledat ve svislé tečné rovině l
odchylku mezi površkou JV a půdorysnou stopou tečné roviny
l (tato stopa s površkou má tedy společný 1.
průmět). Stačí sklopit tečnou rovinu l o
90o do půdorysny (v bodě V1 kolmo k 1.
průmětu površky vyneseme z-ovou souřadnici vrcholu), označíme sklopený bod
(J). Spojením J(V) získáme sklopenou površku a ve sklopení
uvidíme i její odchylku j od půdorysné stopy.
Opět odchylku j přeneseme kružítkem do sítě
(ve správném smyslu, podle průběhu rozvinuté hrany), nové rameno přeneseného
úhlu je už inflexní tečna.
Konec příkladu
RNDr.Pavel Talanda,v.r.
Aktualizace dne 21.05.2002
Copyright © Jan J. Šafařík