Deskriptivní geometrie, I. ročník kombinovaného studia FAST
Pokyny k základním úlohám PERSPEKTIVA - část 2
Obrázky jsou komentovány postupně, některé jsou očíslovány podle základních úloh PERSPEKTIVA. Zde uváděný komentář k obrázkům přebírá čísla 1 až 9, dále 16 až 20, uváděná shodně v příloze obrázků.
Kliknutím otevřete obrázek k úloze ve zvláštním okně v plné velikosti.
Obr. 16 - Měření délky úsečky, je-li tato umístěna na hloubkové přímce v hloubce prostoru příliš daleko Obr. 17 - Sklopení hloubkové přímky (a tudíž následné měření délky úsečky), je-li distance (jak předpis doporučuje) již větší Obr. 19 - Stejnou metodou (sklopeného půdorysu) je sestrojen celý čtverec Obr. 18 - Perspektiva vertikální kružnice
Princip je i na obr. 19. V obr. 18. bude kružnice ve vertikální rovině, avšak šikmo umístěné vzhledem k průmětně (tj.horizontální přímky se sbíhají do bodu Ubs a nikoli do bodu H). Je dán střed Os (také svým půdorysem Os,1), dále poloměr r = 30Obr. 20 - Kružnice v základní rovině p
Kliknutím na obrázek získáte jeho plnou velikost ve zvláštním okně
| Úloha č. 16: | Měření délky úsečky, je-li tato umístěna na hloubkové přímce v hloubce prostoru příliš daleko: |
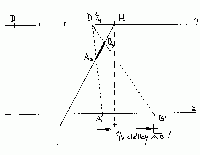 Kdybychom použili jako dělicí bod levý distančník Dl,
pak by promítací přímky zasáhly základnici mimo rozsah nákresny (=papíru).
Zde se využívá jednoduchých vlastností ze stejnolehlosti. Z tzv.
"čtvrtinového distančníku", označen D/4 získáme na základnici
zase jen čtvrtinu A'B' skutečné velikosti úsečky.
(Jako střed uvedené stejnolehlosti vezměme hlavní bod H.)
Kdybychom použili jako dělicí bod levý distančník Dl,
pak by promítací přímky zasáhly základnici mimo rozsah nákresny (=papíru).
Zde se využívá jednoduchých vlastností ze stejnolehlosti. Z tzv.
"čtvrtinového distančníku", označen D/4 získáme na základnici
zase jen čtvrtinu A'B' skutečné velikosti úsečky.
(Jako střed uvedené stejnolehlosti vezměme hlavní bod H.)
| Úloha č. 17: | Sklopení hloubkové přímky (a tudíž následné měření délky úsečky), je-li distance (jak předpis doporučuje) již větší: |
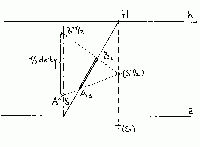 Sklopená hloubková přímka bude kolmá k základnici a bude procházet
stopníkem N perspektivního průmětu přímky.
Místo bodu (S) užijeme např. poloviční distance a tudíž
bodu (S/2). Opět i nyní je sklopený obraz a jeho perspektivní
průmět v kolineárním vztahu [pro osu kolineace =
základnici z a pro střed kolineace (S/2)]. Úsečka
s koncovými body A´/2 , B´/2 je v poloviční velikosti.
Rozhodující je vzdálenost např. (S/4) od bodu H: půjde ovšem jen o jednu čtvrtinu a nikoli o tři čtvrtiny skutečné délky úsečky!
Sklopená hloubková přímka bude kolmá k základnici a bude procházet
stopníkem N perspektivního průmětu přímky.
Místo bodu (S) užijeme např. poloviční distance a tudíž
bodu (S/2). Opět i nyní je sklopený obraz a jeho perspektivní
průmět v kolineárním vztahu [pro osu kolineace =
základnici z a pro střed kolineace (S/2)]. Úsečka
s koncovými body A´/2 , B´/2 je v poloviční velikosti.
Rozhodující je vzdálenost např. (S/4) od bodu H: půjde ovšem jen o jednu čtvrtinu a nikoli o tři čtvrtiny skutečné délky úsečky!
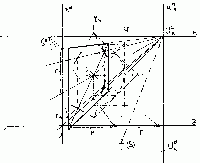
| Úloha č. 19 : | Stejnou metodou (sklopeného půdorysu) je sestrojen celý čtverec. Útvary Do/2 a Ds jsou kolineární dvojicí, kdežto útvary Do a Do/2 jsou v obyčejném afinním vztahu. Toto si dobře promyslete! |
 Návod: protažením úsečky AsBs k horizontu
h je nalezen úběžník této přímky a na základnici stopník této přímky.
Spojením úběžníku se sklopeným středem (S) je sestrojena sklopená
směrová přímka. Dále je ve stopníku vedena rovnoběžka se sklopenou směrovou
přímkou. Mezi sklopeným půdorysem a perspektivním průmětem je kolineární
vztah. Středem kolineace je sklopený střed (S), osou kolineace
je základnice z a horizont h slouží jako úběžnice. Pozor,
ale jen pro útvary v "poli", s označením indexem
"s", tj. pro útvary, které existují jako perspektivními
průměty. Kolineárními paprsky (vedenými ze středu kolineace (S)
jsou body As a Bs promítnuty do
kolineárních bodů Ao a Bo. Toto je už
strana čtverce pro sklopený půdorys. Po dorýsování celého čtverce je zpětně
vedena v bodě Do sklopená hloubková přímka
mo (kolmo k základnici), až po její stopník
(= v kolineaci tedy samodružný bod). Tento bod na základnici je
zpětně spojen s hlavním bodem H. Tak vznikne perspektivní
průmět ms hloubkové přímky. Propojením bodu
Do a středu kolineace (S) vznikne kolineární
paprsek a na něm musí být i kolineární bod Ds
k bodu Do. Podobně je propojen
Co a Cs. Dvě protější strany čtverce:
DoCo a AoBo podají
na základnici samodružné body. A z těchto samodružných bodů vedeme
perspektivní (nyní kolineární) průměty do společného úběžníku (na pravé
straně). Nyní rozpůlme vzdálenost distance H(S) a najděme
tzv."poloviční" sklopený (S1/2). Zbývá se zmínit, že ke sklopenému
obrazu čtverce Ao...Do je kolineární útvar
(jeví se nyní jako kosodélník) Ao1/2...Do1/2.
Středem kolineace bude právě "poloviční sklopený střed (S1/2).
Užívá se zejména tehdy, když je buď veliká distance (a sklopený
(S) vychází mimo nákresnu) nebo když je sklopený útvar = čtverec
sám o sobě veliký a také tudíž vychází mimo nákresnu.
Rýsování "polovičního sklopeného útvaru = kosodélníka" je možné si usnadnit:
je totiž ve vztahu kolmé osové afinity se sklopeným útvarem = čtvercem a
osou afinity je základnice z. V praxi bychom nejdříve vyrýsovali
aspoň některé ještě dostupné body Do... (které ještě
vycházejí na nákresně). Dále bychom afinitou mezi Do a
Do1/2 odvodili celý, kompletní "sklopený útvar
s body Do1/2...zde stále ještě označovaný jako tzv.
"poloviční" u nás např. kosodélník. Konečně bychom využili kolineárního
vztahu mezi tímto celým vyrýsovaným "polovičním sklopeným útvarem" =
kosodélníkem a hledaným perspektivním průmětem, tj. např. mezi body
Co a Cs.
Návod: protažením úsečky AsBs k horizontu
h je nalezen úběžník této přímky a na základnici stopník této přímky.
Spojením úběžníku se sklopeným středem (S) je sestrojena sklopená
směrová přímka. Dále je ve stopníku vedena rovnoběžka se sklopenou směrovou
přímkou. Mezi sklopeným půdorysem a perspektivním průmětem je kolineární
vztah. Středem kolineace je sklopený střed (S), osou kolineace
je základnice z a horizont h slouží jako úběžnice. Pozor,
ale jen pro útvary v "poli", s označením indexem
"s", tj. pro útvary, které existují jako perspektivními
průměty. Kolineárními paprsky (vedenými ze středu kolineace (S)
jsou body As a Bs promítnuty do
kolineárních bodů Ao a Bo. Toto je už
strana čtverce pro sklopený půdorys. Po dorýsování celého čtverce je zpětně
vedena v bodě Do sklopená hloubková přímka
mo (kolmo k základnici), až po její stopník
(= v kolineaci tedy samodružný bod). Tento bod na základnici je
zpětně spojen s hlavním bodem H. Tak vznikne perspektivní
průmět ms hloubkové přímky. Propojením bodu
Do a středu kolineace (S) vznikne kolineární
paprsek a na něm musí být i kolineární bod Ds
k bodu Do. Podobně je propojen
Co a Cs. Dvě protější strany čtverce:
DoCo a AoBo podají
na základnici samodružné body. A z těchto samodružných bodů vedeme
perspektivní (nyní kolineární) průměty do společného úběžníku (na pravé
straně). Nyní rozpůlme vzdálenost distance H(S) a najděme
tzv."poloviční" sklopený (S1/2). Zbývá se zmínit, že ke sklopenému
obrazu čtverce Ao...Do je kolineární útvar
(jeví se nyní jako kosodélník) Ao1/2...Do1/2.
Středem kolineace bude právě "poloviční sklopený střed (S1/2).
Užívá se zejména tehdy, když je buď veliká distance (a sklopený
(S) vychází mimo nákresnu) nebo když je sklopený útvar = čtverec
sám o sobě veliký a také tudíž vychází mimo nákresnu.
Rýsování "polovičního sklopeného útvaru = kosodélníka" je možné si usnadnit:
je totiž ve vztahu kolmé osové afinity se sklopeným útvarem = čtvercem a
osou afinity je základnice z. V praxi bychom nejdříve vyrýsovali
aspoň některé ještě dostupné body Do... (které ještě
vycházejí na nákresně). Dále bychom afinitou mezi Do a
Do1/2 odvodili celý, kompletní "sklopený útvar
s body Do1/2...zde stále ještě označovaný jako tzv.
"poloviční" u nás např. kosodélník. Konečně bychom využili kolineárního
vztahu mezi tímto celým vyrýsovaným "polovičním sklopeným útvarem" =
kosodélníkem a hledaným perspektivním průmětem, tj. např. mezi body
Co a Cs.
| Úloha č. 18: | Perspektiva vertikální kružnice. Princip je i na obr. 19. V obr. 18. bude kružnice ve vertikální rovině, avšak šikmo umístěné vzhledem k průmětně (tj.horizontální přímky se sbíhají do bodu Ubs a nikoli do bodu H). Je dán střed Os (také svým půdorysem Os,1), dále poloměr r = 30: |
 Pokyny: Nejdříve vedeme bodem Os,1 průsečnici
bs základní roviny p
a roviny a, ve které bude ležet kružnice.
Protože rovina a musí být vertikální, bude
její úběžnice uas také
vertikální a bude vedena úběžníkem Ubs. Stopník
N průsečnice bs leží na základnici z. Protože
přímkou bs bude procházet vertikální rovina
a, vedeme stopu
pa roviny
a svisle stopníkem N přímky
bs. Dále zavedeme středem Os přímku
qs vertikální (když bude qs rovnoběžná
se stopou pa, bude průčelná.
Poloměr na ni vyneseme pomoci jejího přesunutí na stopu
pa, od bodu O'na obě
strany "r" a zpět. Průměr, kolmý k přímce qs,
bude horizontální a bude tudíž ležet na přímce
gs=OsUbs. Tento průměr
omezíme nejdříve na půdoryse Os,1 (protože délka
horizontální úsečky je shodná s délkou jejího půdorysu) a sice pomocí
dělicího bodu
QbºSo. Po
nalezení bodu O'1 (promítnutím bodu Os,1
z dělicího bodu Qb k základnici z) , a
posléze vyznačíme úsečku O'1L'1 = r, takže
z bodu L´1 odvodíme (přes Qb)
zpětně bod Ls,1 a na kolmici také i Ls.
Stejně bychom došli i k bodu na druhé straně od bodu
Os. -- Bod Ms výškou 0.7 krát
poloměr nad úrovní bodu Os (viz dolní náčrtek). Užijeme
obou úhlopříček a dalším bodům.
Pokyny: Nejdříve vedeme bodem Os,1 průsečnici
bs základní roviny p
a roviny a, ve které bude ležet kružnice.
Protože rovina a musí být vertikální, bude
její úběžnice uas také
vertikální a bude vedena úběžníkem Ubs. Stopník
N průsečnice bs leží na základnici z. Protože
přímkou bs bude procházet vertikální rovina
a, vedeme stopu
pa roviny
a svisle stopníkem N přímky
bs. Dále zavedeme středem Os přímku
qs vertikální (když bude qs rovnoběžná
se stopou pa, bude průčelná.
Poloměr na ni vyneseme pomoci jejího přesunutí na stopu
pa, od bodu O'na obě
strany "r" a zpět. Průměr, kolmý k přímce qs,
bude horizontální a bude tudíž ležet na přímce
gs=OsUbs. Tento průměr
omezíme nejdříve na půdoryse Os,1 (protože délka
horizontální úsečky je shodná s délkou jejího půdorysu) a sice pomocí
dělicího bodu
QbºSo. Po
nalezení bodu O'1 (promítnutím bodu Os,1
z dělicího bodu Qb k základnici z) , a
posléze vyznačíme úsečku O'1L'1 = r, takže
z bodu L´1 odvodíme (přes Qb)
zpětně bod Ls,1 a na kolmici také i Ls.
Stejně bychom došli i k bodu na druhé straně od bodu
Os. -- Bod Ms výškou 0.7 krát
poloměr nad úrovní bodu Os (viz dolní náčrtek). Užijeme
obou úhlopříček a dalším bodům.
| Úloha č. 20: | Kružnice v základní rovině p: |
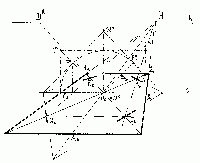 Jde o obdobu obr. 18. Po vyrýsování čtverce s dotykovými body:
As, Bs,Cs,Ds vyhledáme
např. okamžitou průčelnou polohou půlkružnice nad průměrem
CsDs. Všimněme si, že úhlopříčky (které vytínají
body Es, Js, Gs a
Fs) procházejí distančníkem levým:
Dl, případně (není vyrýsováno) distančníkem
pravým Dp. Tečna v bodě Eo
nám podává samodružný bod na ose "lokálního" otočení
CsDs. Z něj lze ihned vést do bodu
Es perspektivní průmět tečny, atd.
Jde o obdobu obr. 18. Po vyrýsování čtverce s dotykovými body:
As, Bs,Cs,Ds vyhledáme
např. okamžitou průčelnou polohou půlkružnice nad průměrem
CsDs. Všimněme si, že úhlopříčky (které vytínají
body Es, Js, Gs a
Fs) procházejí distančníkem levým:
Dl, případně (není vyrýsováno) distančníkem
pravým Dp. Tečna v bodě Eo
nám podává samodružný bod na ose "lokálního" otočení
CsDs. Z něj lze ihned vést do bodu
Es perspektivní průmět tečny, atd.
RNDr. Pavel Talanda,
Ústav matematiky a deskriptivy
Fakulta stavební Brno
Aktualizace dne 03.06.2002
Copyright © Ústav Ma-DG

