Deskriptivní geometrie, I. ročník kombinovaného studia FAST
Pokyny k základním úlohám PERSPEKTIVA - část 1
Obrázky jsou komentovány postupně, některé jsou očíslovány podle základních úloh PERSPEKTIVA. Zde uváděný komentář k obrázkům přebírá čísla 1 až 9, dále 16 až 20, uváděná shodně v příloze obrázků.
Kliknutím otevřete obrázek k úloze ve zvláštním okně v plné velikosti.
Obr. 1 - Skutečná velikost úsečky. Obr. 2 - Kolmice b z bodu A na přímku a - vše leží v horizontální rovině. Obr. 3 - Měření úseček na hloubkových přímkách. Obr. 4 - Sestrojte vodorovné přímky, procházející body As, Bs, Cs a sice takové, aby ve skutečnosti svíraly tentýž úhel 60o s danou přímkou as. Obr. 5 - Měření délek na přímce "frontální", "průčelné", tj. rovnoběžné s průmětnou, ale navíc skloněné k základní rovině p (např. úlopříčky průčelného obdélníka). Obr. 6 - Vzdálenost dvou rovnoběžných přímek, které však nejsou už hloubkové. Obr. 7 - Krychle je určena danou horizontální hranou AsBs, (která je navíc ještě rovnoběžná se základnicí). Obr. 8 - Úhel dvou horizontálních různoběžek asbs. Obr. 9 - Sestrojte horizontální čtverec, je-li dán průmět jeho strany AsBs.
Kliknutím na obrázek získáte jeho plnou velikost ve zvláštním okně
| Úloha č. 1: | Skutečná velikost úsečky: |
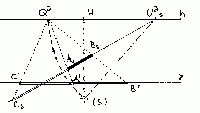 Je dán perspektivní průmět úsečky s koncovými body
AsBs. Prodloužíme úsečku k horizontu,
až obdržíme úběžník Uas této přímky
as (na horizontu proto, že předpokládáme vodorovnou polohu
úsečky). Kružítko zabodneme do tohoto úběžníku, kružnici bude procházet
sklopeným středem (S). Vytočíme na horizont, tato kružnice se
jmenuje "dělicí" a vyznačí na horizontu dělicí bod Qa
(index musí být totožný s indexem "a", který je
u úběžníku = středu Uas této dělicí
kružnice). Body As, Bs z tohoto dělicího
bodu Qa promítneme na základnici z do bodů, které
označíme A', B'. Jejich vzdálenost je už
skutečná velikost úsečkyAB.
Je dán perspektivní průmět úsečky s koncovými body
AsBs. Prodloužíme úsečku k horizontu,
až obdržíme úběžník Uas této přímky
as (na horizontu proto, že předpokládáme vodorovnou polohu
úsečky). Kružítko zabodneme do tohoto úběžníku, kružnici bude procházet
sklopeným středem (S). Vytočíme na horizont, tato kružnice se
jmenuje "dělicí" a vyznačí na horizontu dělicí bod Qa
(index musí být totožný s indexem "a", který je
u úběžníku = středu Uas této dělicí
kružnice). Body As, Bs z tohoto dělicího
bodu Qa promítneme na základnici z do bodů, které
označíme A', B'. Jejich vzdálenost je už
skutečná velikost úsečkyAB.
| Úloha č. 2: | Kolmice b z bodu A na přímku a - vše leží v horizontální rovině: |
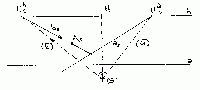 Sestrojíme sklopený směrový paprsek (či "směrovou přímku"), označenou
(a´) nebo také (a), tj. namísto "apostrofu" se označuje také
pruhem nad písmenem - jako spojnici sklopeného středu (S) a úběžníku
(Uas) přímky as. Protože
požadovaná kolmice b musí mít svoji směrovou přímku b'
kolmou ke směrové přímce a', musí se ve sklopení tento pravý úhel
projevit ve skutečné velikosti. Připravíme tudíž nejdříve sklopenou směrovou
přímku (b'): vedeme ji sklopeným středem (S) kolmo ke
sklopené směrové přímce (a') -- opět sklopeným středem (S).
Tato další přímka (b') vytne na horizontu (protože je rovněž
vodorovná) další úběžník Ubs. Perspektivní
průmět bs hledané přímky b musí tímto novým
úběžníkem procházet. Prochází ovšem i daným bodem As,
tj. bs = AsUbs.
Sestrojíme sklopený směrový paprsek (či "směrovou přímku"), označenou
(a´) nebo také (a), tj. namísto "apostrofu" se označuje také
pruhem nad písmenem - jako spojnici sklopeného středu (S) a úběžníku
(Uas) přímky as. Protože
požadovaná kolmice b musí mít svoji směrovou přímku b'
kolmou ke směrové přímce a', musí se ve sklopení tento pravý úhel
projevit ve skutečné velikosti. Připravíme tudíž nejdříve sklopenou směrovou
přímku (b'): vedeme ji sklopeným středem (S) kolmo ke
sklopené směrové přímce (a') -- opět sklopeným středem (S).
Tato další přímka (b') vytne na horizontu (protože je rovněž
vodorovná) další úběžník Ubs. Perspektivní
průmět bs hledané přímky b musí tímto novým
úběžníkem procházet. Prochází ovšem i daným bodem As,
tj. bs = AsUbs.
| Úloha č. 3 : | Měření úseček na hloubkových přímkách: |
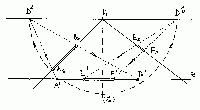 Jejich úběžníkem je hlavním bod H a přímky jsou v prostoru kolmé
k perspektivní průmětně. Proto pohlížíme na hlavní bod H jako
na úběžník: Zabodneme do něj kružítko a teď opíšeme kružnici sklopeným
středem (S). Poloměr této kružnice bude vyjímečně roven distanci.
Průsečík s horizontem se tudíž může nazývat levý (resp. pravý)
distančník , Dl, resp. Dp. Tento bod
má proto funkci dělicího bodu právě pro hloubkové přímky. Obdobně - jako
u obr. 1 - promítáme z tohoto dělicího bodu
Dl body As, Bs a zase
z pravého distančníku Dp také body
Es, Fs. Vybíráme ten ze dvou distančníků,
u kterého polohy promítacích přímek jsou příznivější (mají větší
úhel s příslušnou hloubkovou přímkou), aby se udržela co největší
přesnost při rýsování.
Jejich úběžníkem je hlavním bod H a přímky jsou v prostoru kolmé
k perspektivní průmětně. Proto pohlížíme na hlavní bod H jako
na úběžník: Zabodneme do něj kružítko a teď opíšeme kružnici sklopeným
středem (S). Poloměr této kružnice bude vyjímečně roven distanci.
Průsečík s horizontem se tudíž může nazývat levý (resp. pravý)
distančník , Dl, resp. Dp. Tento bod
má proto funkci dělicího bodu právě pro hloubkové přímky. Obdobně - jako
u obr. 1 - promítáme z tohoto dělicího bodu
Dl body As, Bs a zase
z pravého distančníku Dp také body
Es, Fs. Vybíráme ten ze dvou distančníků,
u kterého polohy promítacích přímek jsou příznivější (mají větší
úhel s příslušnou hloubkovou přímkou), aby se udržela co největší
přesnost při rýsování.
| Úloha č. 4: | Sestrojte vodorovné přímky, procházející body As, Bs, Cs a sice takové, aby ve skutečnosti svíraly tentýž úhel 60o s danou přímkou as: |
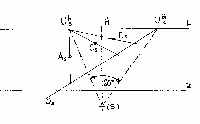 Je zřejmé, že takové přímky budou mezi sebou rovnoběžné a budou mít společný
úběžník Ubs. Nejdříve sklopíme směrovou přímku
(a') dané přímky as. I zde platí:
(a') = (S)Uas. Úhel 60o
ve skutečné hodnotě ukáží obě sklopené směrové přímky. Proto novou sklopenou
směrovou přímku (b') = narýsujeme s odklonem požadovaného úhlu
(např. v kladném smyslu měření úhlu). Nejdříve tedy obdržíme (b')
a tato vytne na horizontu nový úběžník Ubs.
Nyní už stačí postupně spojit každý daný bod
As,Bs,Cs s úběžníkem
Ubs.
Je zřejmé, že takové přímky budou mezi sebou rovnoběžné a budou mít společný
úběžník Ubs. Nejdříve sklopíme směrovou přímku
(a') dané přímky as. I zde platí:
(a') = (S)Uas. Úhel 60o
ve skutečné hodnotě ukáží obě sklopené směrové přímky. Proto novou sklopenou
směrovou přímku (b') = narýsujeme s odklonem požadovaného úhlu
(např. v kladném smyslu měření úhlu). Nejdříve tedy obdržíme (b')
a tato vytne na horizontu nový úběžník Ubs.
Nyní už stačí postupně spojit každý daný bod
As,Bs,Cs s úběžníkem
Ubs.
| Úloha č. 5: | Měření délek na přímce "frontální", "průčelné", tj. rovnoběžné s průmětnou, ale navíc skloněné k základní rovině p (např. úlopříčky průčelného obdélníka): |
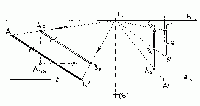 Je dán průmět úsečky AsBs a přitom platí,
že B1s = Bs, takže bod B leží
v základní rovině p. Tento bod
přesuneme např. hloubkovou přímkou (místo bodu H ale můžeme však
zvolit každý jiný dostupný úběžník) na základnici a označíme jako
B´. V druhém koncovém bodě As zavedeme další
hloubkovou přímku (v případě volby obecného úběžníku by vedla zase
takovým obecným). Tuto druhou přímku jen přiměřeně protáhneme.
Z prostoru přijmeme poznatek, že průčelná přímka (tedy fakticky
rovnoběžná s perspektivní průmětnou se po přesunu jako celek umístí
v perspektivní průmětně a bude rovnoběžná se svým původní polohou,
tedy i se svým původním perspektivním průmětem. Proto vedeme bodem
B´ (na základnici) rovnoběžku "a" s přímkou
AsBs a to tak dalece, až se protne
s připravenou hloubkovou přímkou (vedenou bodem As)
v bodě A´.
Je dán průmět úsečky AsBs a přitom platí,
že B1s = Bs, takže bod B leží
v základní rovině p. Tento bod
přesuneme např. hloubkovou přímkou (místo bodu H ale můžeme však
zvolit každý jiný dostupný úběžník) na základnici a označíme jako
B´. V druhém koncovém bodě As zavedeme další
hloubkovou přímku (v případě volby obecného úběžníku by vedla zase
takovým obecným). Tuto druhou přímku jen přiměřeně protáhneme.
Z prostoru přijmeme poznatek, že průčelná přímka (tedy fakticky
rovnoběžná s perspektivní průmětnou se po přesunu jako celek umístí
v perspektivní průmětně a bude rovnoběžná se svým původní polohou,
tedy i se svým původním perspektivním průmětem. Proto vedeme bodem
B´ (na základnici) rovnoběžku "a" s přímkou
AsBs a to tak dalece, až se protne
s připravenou hloubkovou přímkou (vedenou bodem As)
v bodě A´.
Vertikální úsečka BsCs má svůj průsečík
(tj."kořen") se základní rovinou p
v bodě As. Při jejím přesunu do průmětny
musíme však dbát, aby tento bod As byl přesunut na
základnici z, do polohy A´. Toto opět můžeme
vykonat jakoukoli přímkou - zde byla však použita přímka hloubková.
V průmětně stanovíme v bodě A´ vertikální přímku
a dodatečně až k této protáhneme hloubkové přímky, vedené body
Bs, Cs. Obdržíme pak v průmětně body
B´, C´ . Protože tyto body leží v průmětně, tak jejich
vzdálenost je už skutečná velikost úsečky AB.
| Úloha č. 6: | Vzdálenost dvou rovnoběžných přímek, které však nejsou už hloubkové: |
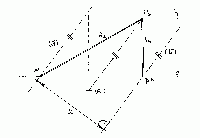 Je více způsobů, jak lze šířku mezi těmito přímkami as,
bs poměřovat. Užijme např. metody "sklopeného půdorysu"
těchto přímek: sestrojíme sklopenou směrovou přímku (a´) jako
spojnici (S) s úběžníkem přímek Us.
Označme pro sklápění samodružné body těchto přímek - jsou to jejich
stopníky Pa a Pb. V těchto
stopnících povedeme rovnoběžky se sklopenou směrovou přímkou - přímky
(a), (b) budou proto spolu rovnoběžné. Šířka mezi těmito
sklopenými přímkami je hledaná vzdálenost.
Je více způsobů, jak lze šířku mezi těmito přímkami as,
bs poměřovat. Užijme např. metody "sklopeného půdorysu"
těchto přímek: sestrojíme sklopenou směrovou přímku (a´) jako
spojnici (S) s úběžníkem přímek Us.
Označme pro sklápění samodružné body těchto přímek - jsou to jejich
stopníky Pa a Pb. V těchto
stopnících povedeme rovnoběžky se sklopenou směrovou přímkou - přímky
(a), (b) budou proto spolu rovnoběžné. Šířka mezi těmito
sklopenými přímkami je hledaná vzdálenost.
| Úloha č. 7: | Krychle je určena danou horizontální hranou AsBs (která je navíc ještě rovnoběžná se základnicí): |
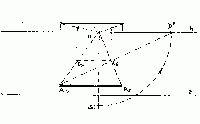 Sousední hrany čtvercové podstavy jsou k hraně AB kolmé a
tudíž jsou i kolmé k základnici z. Proto jsou hloubkové
přímky o společném úběžníku v hlavním bodě H.
Všimněme si funkce průsečíku Dp
horizontu h s distanční kružnicí
(o středu H a poloměru rovném distanci d).
Nazývá se "(pravý) distančník".
Sousední hrany čtvercové podstavy jsou k hraně AB kolmé a
tudíž jsou i kolmé k základnici z. Proto jsou hloubkové
přímky o společném úběžníku v hlavním bodě H.
Všimněme si funkce průsečíku Dp
horizontu h s distanční kružnicí
(o středu H a poloměru rovném distanci d).
Nazývá se "(pravý) distančník".
* Je za a) : úběžníkem horizontálních přímek, které navíc svírají
s průmětnou odchylku 45o (= tedy např.
úhlopříčky horizontálních čtverců s průčelnými a hloubkovými stranami).
* Dále je za b) : bod Dp je i dělicím bodem hloubkových
přímek.
Využijeme za a): bodem As vedeme do
úběžníku Dp úhlopříčku. Ta vytne na hloubkové přímce
bod Cs. Stačí na rovnoběžce doplnit snadno i bod
Ds. Nad tímto čtvercem vztyčíme především průčelný
čtverec AsBsFsEs
(stejné délky stran a pravé úhly jsou vždy u průčelného čtverce
zachovány - i když "za osou x" zmenšeny oproti skutečnosti).
Už jenom s použitím snadného principu rovnoběžnosti hran - a tudíž
sbíhavosti do bodu H doplníme další dva chybějící vrcholy.
| Úloha č.8: | Úhel dvou horizontálních různoběžek asbs: |
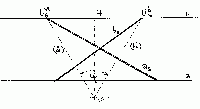 Připomeňme si, že směrové přímky a'//a, b'//b jsou
s danými přímkami a, b v prostoru rovnoběžné (a
procházejí středem promítání S). Proto i tyto směrové přímky
svírají stejnou odchylku a jako
přímky původní. Tyto směrové přímky můžeme nejen okamžitě uvážit - jako
spojnice: a' = SUas,
b' = SUbs, ale také ihned sklopit
(z jejich horizontální roviny, procházející horizontem h
a středem S) o 90o dolů do perspektivní
průmětny. Stačí totiž spojit sklopený střed (S) s oběma
úběžníky. Úhel a mezi sklopenými
směrovými přímkami (a'), (b') je již hledaná odchylka.
Připomeňme si, že směrové přímky a'//a, b'//b jsou
s danými přímkami a, b v prostoru rovnoběžné (a
procházejí středem promítání S). Proto i tyto směrové přímky
svírají stejnou odchylku a jako
přímky původní. Tyto směrové přímky můžeme nejen okamžitě uvážit - jako
spojnice: a' = SUas,
b' = SUbs, ale také ihned sklopit
(z jejich horizontální roviny, procházející horizontem h
a středem S) o 90o dolů do perspektivní
průmětny. Stačí totiž spojit sklopený střed (S) s oběma
úběžníky. Úhel a mezi sklopenými
směrovými přímkami (a'), (b') je již hledaná odchylka.
| Úloha č. 9: | Sestrojte horizontální čtverec, je-li dán průmět jeho strany AsBs: |
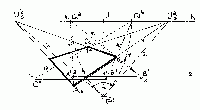 Výjímečně je zde (z důvodu ukázky metodické pomůcky) postup očíslován.
Prodloužením přímky AsBs k horizontu
získáme úběžník Uas. Připojíme sklopenou
směrovou přímku (a') = (S)Uas , tj.
jako spojnici bodu (S) se získaným úběžníkem. Připojíme kolmo
k přímce (a') bodem (S) další sklopenou směrovou
přímku (b') a ta vytne na horizontu další
úběžník Ubs. Propojením
AsUbs a posléze i
BsUbs získáme průměty dvou
rovnoběžných přímek, které jsou v prostoru také ještě kolmé i
k určující straně AsBs.
Výjímečně je zde (z důvodu ukázky metodické pomůcky) postup očíslován.
Prodloužením přímky AsBs k horizontu
získáme úběžník Uas. Připojíme sklopenou
směrovou přímku (a') = (S)Uas , tj.
jako spojnici bodu (S) se získaným úběžníkem. Připojíme kolmo
k přímce (a') bodem (S) další sklopenou směrovou
přímku (b') a ta vytne na horizontu další
úběžník Ubs. Propojením
AsUbs a posléze i
BsUbs získáme průměty dvou
rovnoběžných přímek, které jsou v prostoru také ještě kolmé i
k určující straně AsBs.
* Nyní je na místě už změřit skutečnou velikost strany
AsBs. K tomu použijeme dělicího
bodu Qa. [Bude to průsečík horizontu s dělicí
kružnicí. Dělicí kružnice má svůj střed v úběžníku
Uas a poloměr
(S)Uas. Tedy tato kružnice prochází bodem
(S).] Ze získaného dělicího bodu Qa (označení
indexy "a" musí být důsledné - podle indexu
u úběžníku Uas) promítáme koncové
body AsBs až na základnici z.
Vzdálenost mezi získanými průsečíky A' B' promítacích přímek
na z je skutečná velikost úsečky.
*Abychom našli třetí bod Cs, musíme užít úlohu:
"z bodu Bs naneste na přímku
bs jistou velikost, tj. A'B' a to od bodu
Bs (ve smyslu: do hloubky prostoru)". Učiníme tak za
pomoci nového dělicího bodu, který bude příslušný k této přímce
bs, přesněji: k jejímu úběžníku
Ubs (tedy nová dělicí kružnice má svůj střed
v tomto úběžníku Ubs, prochází zase
sklopeným bodem (S) a vytne na horizontu dělicí bod
Qb). Nejdříve užijeme promítací přímku z dělicího
bodu Qb přes Bs až získáme
tak na základnici první bod B'' (dva apostrofy užíváme pro
odlišení od dřívějšího B', tj. s jedním apostrofem a
dřívější akce). Od bodu B'' na základnici doleva, (tj. podle
smyslu úsečky v prostoru) naneseme skutečnou velikost strany čtverce:
kde ji máme uloženou? Je to ovšem úsečka A'B' z dřívější
akce na z. Takže přeneseme její délku a od bodu
B'' nalevo vyhledáme na základnici další bod C'', aby
vzdálenost B''C'' byla stejná. Zpětným promítáním z dělicího
bodu Qb získáme na přímce bs
třetí bod Cs. Konečně čtvrtý bod
Ds získáme podle principu rovnoběžnosti, protože strana
DsCs a AsBs
se sbíhají v úběžníku Uas.
RNDr. Pavel Talanda,
Ústav matematiky a deskriptivy
Fakulta stavební Brno
Aktualizace dne 03.06.2002
Copyright © Ústav Ma-DG

