Fakulta informatiky Masarykovy univerzity v Brně
Jan
Pešl
V teorii pravděpodobnosti předpokládáme, že známe zákon
rozdělení
náhodné veličiny ![]() , tj. známe její distribuční funkci, resp. rozdělovací
funkci. V technických aplikacích se často stává, že jsme v situaci,
že rozdělení náhodné veličiny
, tj. známe její distribuční funkci, resp. rozdělovací
funkci. V technických aplikacích se často stává, že jsme v situaci,
že rozdělení náhodné veličiny ![]() neznáme, ale pouze se domníváme, že by náhodná
veličina
neznáme, ale pouze se domníváme, že by náhodná
veličina ![]() mohla mít určité rozdělení (např. normální), nebo dokonce nemáme
žádnou
konkrétní představu o rozdělení náhodné veličiny
mohla mít určité rozdělení (např. normální), nebo dokonce nemáme
žádnou
konkrétní představu o rozdělení náhodné veličiny ![]() .
.
Představu o rozdělení náhodné veličiny ![]() můžeme získat např. z histogramu
relativních četností. Podle jeho tvaru lze usuzovat na tvar rozdělovací
funkce náhodné veličiny
můžeme získat např. z histogramu
relativních četností. Podle jeho tvaru lze usuzovat na tvar rozdělovací
funkce náhodné veličiny ![]() . K tomu je zapotřebí jednak sestrojit
histogram, jednak
porovnat tento histogram s
grafy vhodných rozdělovacích
funkcí.
. K tomu je zapotřebí jednak sestrojit
histogram, jednak
porovnat tento histogram s
grafy vhodných rozdělovacích
funkcí.
Je-li vytvořena hypotéza (domněnka) o tvaru rozdělení náhodné
veličiny ![]() ,
přejdeme k některému z testů, kterým tuto hypotézu nezamítneme, resp.
zamítneme s dostatečně malým rizikem omylu. Tyto testy nazýváme testy shody. My se zde budeme zabývat
pouze jedním testem shody - a to Pearsonovým. Je zapotřebí si
uvědomit,
že hypotézu vytvořenou z určité realizace
náhodného výběru z
,
přejdeme k některému z testů, kterým tuto hypotézu nezamítneme, resp.
zamítneme s dostatečně malým rizikem omylu. Tyto testy nazýváme testy shody. My se zde budeme zabývat
pouze jedním testem shody - a to Pearsonovým. Je zapotřebí si
uvědomit,
že hypotézu vytvořenou z určité realizace
náhodného výběru z ![]() bychom správně měli
ještě ověřit na
jiné realizaci
náhodného výběru z
bychom správně měli
ještě ověřit na
jiné realizaci
náhodného výběru z ![]() .
.
Domníváme se, že náhodná veličina ![]() má rozdělovací funkci
má rozdělovací funkci
![]() , kde
, kde
![]() jsou neznámé parametry. Připouštíme i
jsou neznámé parametry. Připouštíme i ![]() , tj. že rozdělovací funkce je
, tj. že rozdělovací funkce je
![]() a nejsou v ní obsaženy žádné neznámé
parametry. Je-li
a nejsou v ní obsaženy žádné neznámé
parametry. Je-li ![]() ,
použijeme realizaci
,
použijeme realizaci
![]() náhodného výběru
náhodného výběru
![]() z
z ![]() pro výpočet
realizací odhadů
parametrů
pro výpočet
realizací odhadů
parametrů
![]() - označme je
- označme je
![]() .
Realizace odhadů dosadíme za parametry do rozdělovací funkce
.
Realizace odhadů dosadíme za parametry do rozdělovací funkce ![]() , dostaneme
rozdělovací funkci
, dostaneme
rozdělovací funkci
![]() ,
která již neobsahuje neznámé parametry. Pearsonův test shody je
pak test hypotézy
,
která již neobsahuje neznámé parametry. Pearsonův test shody je
pak test hypotézy
![]() :
: ![]() má rozdělovací funkci
má rozdělovací funkci
![]() proti hypotéze
proti hypotéze
![]() :
: ![]() nemá rozdělovací funkci
nemá rozdělovací funkci
![]() pro žádný z možných parametrů
pro žádný z možných parametrů
![]() na hladině významnosti
na hladině významnosti ![]() .
.
Postup při samotném testu je následující:
Předpokládáme, že platí hypotéza ![]() , tj. že
náhodná veličina
, tj. že
náhodná veličina ![]() má rozdělovací funkci
má rozdělovací funkci
![]() .
.
Obor hodnot ![]() náhodné veličiny
náhodné veličiny ![]() rozdělíme do
rozdělíme do ![]() disjunktních tříd
disjunktních tříd
![]() . Přitom dodržujeme stejná pravidla jako při
konstrukci histogramu nebo se snažíme roztřídit realizaci do tříd o
přibližně stejné četnosti. Pro označení absolutních četností ponecháme
označení
. Přitom dodržujeme stejná pravidla jako při
konstrukci histogramu nebo se snažíme roztřídit realizaci do tříd o
přibližně stejné četnosti. Pro označení absolutních četností ponecháme
označení
![]() .
.
Označme dále ![]() pravděpodobnost, že náhodná veličina
pravděpodobnost, že náhodná veličina ![]() nabude hodnoty
ze třídy
nabude hodnoty
ze třídy ![]()
![]() za podmínky, že platí hypotéza
za podmínky, že platí hypotéza ![]() , tj.
, tj.
|
|
(1) |
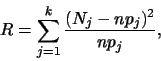 |
(2) |
|
|
(3) |
Místo kritického oboru pro test hypotézy ![]() proti hypotéze
proti hypotéze ![]() na
hladině významnosti
na
hladině významnosti ![]() použijeme výpočet tzv.
použijeme výpočet tzv. ![]() -hodnoty, kdy
vyjádříme pravděpodobnost počítanou za platnosti
nulové hypotézy, že dostaneme právě naši realizaci
-hodnoty, kdy
vyjádříme pravděpodobnost počítanou za platnosti
nulové hypotézy, že dostaneme právě naši realizaci ![]() testovacího kritéria
testovacího kritéria ![]() nebo realizaci ještě více odporující nulové hypotéze. Potom hypotézu
nebo realizaci ještě více odporující nulové hypotéze. Potom hypotézu ![]() zamítneme s rizikem maximálně 100
zamítneme s rizikem maximálně 100![]() procent.
Chceme-li tedy testovat hypotézu
procent.
Chceme-li tedy testovat hypotézu ![]() na hladině významnosti 0.05 a
dostaneme, že
na hladině významnosti 0.05 a
dostaneme, že ![]() , nezamítáme hypotézu
, nezamítáme hypotézu ![]() na hladině významnosti
0.05. Jestliže dostaneme
na hladině významnosti
0.05. Jestliže dostaneme ![]() , hypotézu
, hypotézu ![]() na hladině
významnosti 0.05 zamítáme. Hrubě řečeno, čím větší je
spočtená
na hladině
významnosti 0.05 zamítáme. Hrubě řečeno, čím větší je
spočtená ![]() -hodnota, tím je zamítnutí nulové hypotézy
méně oprávněné.
Zbývá určit, které hodnoty
-hodnota, tím je zamítnutí nulové hypotézy
méně oprávněné.
Zbývá určit, které hodnoty ![]() testovacího kritéria
testovacího kritéria ![]() odporují nulové
hypotéze.
odporují nulové
hypotéze.
Kdyby platila
hypotéza ![]() , pak by pravděpodobnost, že výsledek pokusu
, pak by pravděpodobnost, že výsledek pokusu ![]() nabude hodnoty ze
třídy
nabude hodnoty ze
třídy ![]() , byla
, byla ![]() (viz vztah (1)). Odhad pravděpodobnosti, že
výsledek pokusu padne do třídy
(viz vztah (1)). Odhad pravděpodobnosti, že
výsledek pokusu padne do třídy ![]() , je zřejmě počet příznivých
výsledků ku celkovému počtu možných výsledků - tedy
náhodná veličina
, je zřejmě počet příznivých
výsledků ku celkovému počtu možných výsledků - tedy
náhodná veličina ![]() . Takže v prospěch hypotézy
. Takže v prospěch hypotézy ![]() svědčí ty realizace
svědčí ty realizace ![]() veličiny
veličiny ![]() , které jsou dostatečně blízké číslu
, které jsou dostatečně blízké číslu ![]() ,
tj. pro které
,
tj. pro které
![]() , tj. pro které
, tj. pro které
![]() pro každé
pro každé ![]() .
Číslo
.
Číslo ![]() se někdy
v této souvislosti nazývá empirická četnost
třídy
se někdy
v této souvislosti nazývá empirická četnost
třídy ![]() a číslo
a číslo
![]() pak teoretická četnost třídy
pak teoretická četnost třídy ![]() .
V prospěch hypotézy
.
V prospěch hypotézy ![]() svědčí tedy ty realizace
svědčí tedy ty realizace ![]() testovacího kritéria
testovacího kritéria
![]() , které jsou blízké číslu nula. Nulové hypotéze potom odporují ty
realizace
, které jsou blízké číslu nula. Nulové hypotéze potom odporují ty
realizace ![]() testovacího kritéria
testovacího kritéria ![]() , které jsou větší než nějaká kladná
konstanta.
, které jsou větší než nějaká kladná
konstanta.
Víme, že testovací
kritérium ![]() Pearsonova testu má asymptoticky rozdělení
Pearsonova testu má asymptoticky rozdělení ![]() .
Označme tedy
.
Označme tedy ![]() distribuční funkci tohoto rozdělení, potom pro
distribuční funkci tohoto rozdělení, potom pro ![]() -hodnotu
dostaneme:
-hodnotu
dostaneme:
V případě
spojité náhodné veličiny Použití Pearsonova testu
shody lze procvičit v následujících
příkladech,
které jsou zpracovány v systému Maple.
![]() je třída
je třída ![]() interval.
Označme jeho krajní body jako
interval.
Označme jeho krajní body jako ![]() . Potom pro
. Potom pro
![]() platí
platí
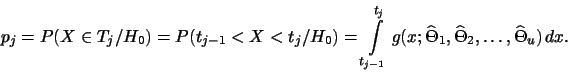
![]() z hustoty
z hustoty ![]() distribuční funkci
distribuční funkci ![]() náhodné veličiny
náhodné veličiny ![]() a pak teprve
počítat
a pak teprve
počítat ![]() . Zřejmě
. Zřejmě
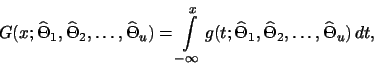
potom
![]()
![]()
V případě
diskrétní náhodné veličiny ![]() je třída
je třída ![]() bod nebo
množina obsahující body oboru hodnot náhodné veličiny
bod nebo
množina obsahující body oboru hodnot náhodné veličiny ![]() .
Je-li
.
Je-li ![]() jeden bod, potom
jeden bod, potom
![]()
Je-li ![]() vícebodová množina bodů, potom
vícebodová množina bodů, potom