Testy shody

Histogram

   Předpokládejme, že máme k dispozici realizaci $(x_1,x_2, \dots, x_n)$ náhodného výběru $(X_1,X_2, \dots, X_n)$ z $X$. Obor hodnot $\Omega$ náhodné veličiny $X$ rozdělíme na $k$ disjunktních tříd - a to následovně:

    1. Je-li $X$ diskrétní náhodná veličina, volíme za třídy $T_j$ jednotlivé body oboru hodnot $\Omega$. Mluvíme o tzv. prostém třídění.

    2. Je-li $X$ spojitá náhodná veličina, volíme za třídy $T_j$ intervaly. Mluvíme o tzv. skupinovém třídění.

    Při třídění pak dodržujeme určitá pravidla. Např.

    a) V případě skupinového třídění se doporučuje, aby intervaly $T_j$ měly stejnou délku a aby hranice a středy tříd byly zaokrouhlená čísla.

    b) Vyskytuje-li se v hraničních třídách velmi málo hodnot, je často vhodné spojit tyto třídy (nebo třídu) se sousední třídou v třídu jedinou.

    c) Doporučuje se, aby počet $k$ výsledných tříd byl 5-20 podle rozsahu výběru $n$ (pokud je to možné). Podle Sturgesova pravidla by pro počet $k$ tříd mělo platit

$$k\doteq 1+3.3\log n .$$

Jiní autoři navrhují

$$k\doteq \sqrt{n},$$

resp.

$$k\leq 5\log n.$$

    Při třídění je vhodné seřadit hodnoty $x_1,x_2, \dots, x_n$ vzestupně (nebo alespoň určit nejmenší a největší zjištěnou hodnotu), abychom získali představu, v jakém rozmezí se tyto hodnoty vyskytují.

    Označme dále $n_j$ počet hodnot, které padly do třídy $T_j$. Číslo $n_j$ nazýváme absolutní četnost třídy $T_j$. Zřejmě

$$n_1+n_2+\dots+n_k=n.$$

Číslo $f_j=n_j/n$ nazýváme relativní četnost třídy $T_j$. Pro relativní četnosti platí

$$f_1+f_2+\dots+f_k=1.$$

Pravděpodobnost, že náhodná veličina $X$ nabude hodnoty ze třídy $T_j$ zřejmě odhadneme relativní četností třídy $T_j$, tj. číslem $f_j$.

    Označme nyní $m(T_j)$ počet prvků, resp. délku třídy $T_j$ v případě prostého, resp. skupinového třídění. Definujme reálnou funkci $g_n$ předpisem

$$g_n(x)=\biggl\{ \begin {array}{c} {\frac{f_j}{m(T_j)}} \quad ... ...ad \quad \quad \quad \quad \quad {\mathrm {jinak}} \end{array}.$$

Funkci $g_n$ nazýváme výběrová rozdělovací funkce náhodné veličiny $X$, její graf nazýváme histogram. Funkce $g_n(x)$ je zřejmě nezáporná funkce proměnné $x$.

    V případě prostého třídění je

$$\sum\limits_{x\in\Omega}g_n(x)=1.$$

Tedy součet nenulových $y$-nových souřadnic bodů histogramu je roven jedné.

    V případě skupinového třídění je součet obsahů obdélníků v histogramu (tj. obsah obrazce ohraničeného osou $x$ a histogramem) roven jedné. Tedy

$$\int\limits_{\Omega}g_n(x)\,dx=1.$$

    Výběrovou rozdělovací funkci náhodné veličiny $X$ lze zřejmě považovat za odhad rozdělovací funkce náhodné veličiny $X$. Takto definovaný histogram je vhodný k porovnávání s grafy teoretických rozdělovacích funkcí.

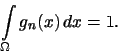
    Častěji se používá histogram relativních četností, resp. absolutních četností, kdy se na osu $x$ nanesou třídy $T_j$ a nad každou třídou se sestrojí "obdélník" o výšce rovné relativní, resp. absolutní četnosti třídy $T_j$. Horní obrys těchto obdélníků je pak histogram relativních, resp. absolutních četností. Nevýhodou těchto histogramů je, že pozbývají vlastnosti rozdělovacích funkcí. Tak např. v případě skupinového třídění nemusí být obsah plochy mezi histogramem relativních četností a osou $x$ roven jedné. Chceme-li mít orientační představu o tvaru teoretické rozdělovací funkce, stačí ale tyto histogramy sestrojit.

    Uvědomme si, že jsme pracovali s realizací náhodného výběru z $X$ a tudíž $n_j$, resp. $f_j$ byly vlastně realizace náhodných veličin $N_j$, resp. $F_j$ a pro každou realizaci náhodného výběru z $X$ dostaneme obecně jiné realizace $n_j, f_j$ a tudíž i jiné histogramy. (Nehledě na to, ze samotné třídění je subjektivní a tudíž pro jedinou realizaci můžeme dostat různé histogramy.)

Testy shody