Příklady metrických prostorů   Obsah

Věta o kontrakci

Definice. Nechť 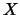je metrický prostor, 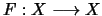a . Zobrazení 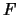se nazývá kontrakce v 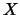s koeficientem 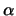, jestliže

Věta 4. (Věta o kontrakci, Banachova věta o pevném bodu) Buďte úplný metrický prostor, kontrakce v s koeficientem , libovolný bod a příslušná posloupnost postupných aproximací. Pak platí

a)

V existuje jediný pevný bod zobrazení .

b)

.

c)

pro

d)

pro

Tvrzení věty 4

a)

zodpovídá otázku existence a jednoznačnosti řešení ÚLOHY,

b)

popisuje postup přibližného řešení ÚLOHY,

c)

říká, že je tím blíže k , čím

• blíže k je ,

• menší je koeficient ,

• větší je index ,

d)

je prakticky použitelný odhad chyby.

 

Důkaz věty 4. 1. JEDNOZNAČNOST: Předpokládejme, že a . Pak užitím D1 dostaneme

2. :

3. pro všechna : Užitím D3 a 2 lze ukázat

4. EXISTENCE: Protože podle 3 platí , pro a libovolné. Tedy posloupnost je cauchyovská. Protože metrický prostor je úplný, existuje . Víme již, že potom je řešením ÚLOHY.
5. :

6. : Podle D3 a 3 platí

   
  Obsah