Ing. Jana Hřebíčková
Mgr. Jaroslav Ráček
Ing. Jana Slaběňáková
Fakulta stavební, Vysoké učení technické
Fakulta informatiky, Masarykova univerzita
Brno
2001
Obsah:
Integrální počet v Maple 7 - mws verze
1. Primitivní funkce,neurčitý integrál - úvod
Příkaz, kter ý vypočítá nerčitý integrál (primitivní funkci) má tvar:
int (výraz, x );
kde jednotlivé parametry znamenají:
výraz - výraz (integrand), který bude integrován
x - proměnná, podle níž se integruje
Pro výpis neurčitého integrálu se používá příkaz Int (výraz, x ).
Při provádění příkazu int zkusí Maple spočítat integrál, ale na rozdíl od výpočtu derivace není zaručena úspěšnost výpočtu. V takovém případě Maple odpoví buď stejným nebo zjednodušeným výrazem, který mu byl zadán k integraci.
Příklady:
Ukážeme si, že funkce F(x) = ![]() je primitivní funkcí k funkci f(x) = 2x v R , neboť (
je primitivní funkcí k funkci f(x) = 2x v R , neboť ( ![]() )' = 2x.
)' = 2x.
> restart;
> Int(2*x,x)=int(2*x,x);
![]()
> Diff(x^2,x)=diff(x^2,x);
![]()
> Int(f(x),x);
![]()
1. způsob výpočtu integrálu:
> int(x+sin(x),x);
![]()
2. způsob:
> F:=Int(x+sin(x),x);
![]()
> value(F);
![]()
3. způsob (modifikace 2. způsobu):
> value(Int(x+sin(x),x));
![]()
Integrál 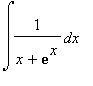 neumí
Maple spočítat analyticky.
neumí
Maple spočítat analyticky.
> int(1/(x+exp(x)),x);
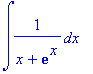
Jednoduchým programem lze získat základní vzorce pro výpočet neurčitých integrálů (bez uvedení definičních oborů):
> f1:=0: f2:=1: f3:=x^n: f4:=1/x: f5:=exp(x): f6:=a^x: f7:=sin(x): f8:=cos(x): f9:=1/cos(x)^2: f10:=1/sin(x)^2: f11:=1/(1+x^2): f12:=1/sqrt(1-x^2): f13:=1/sqrt(x^2+a):
> for i from 1 to 13 do
> Int(f||i,x)=int(f||i,x)
> od;
![]()
![]()
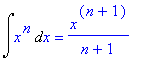
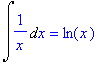
![]()
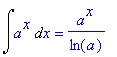
![]()
![]()
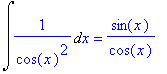
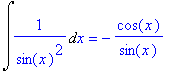
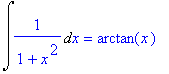
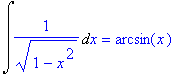
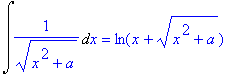
>
2. Integrační metoda po částech (per partes) pro neurčitý integrál
Platí vzorec 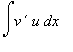 =
= 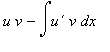
V Maplu se užívá funkce intparts(g, u), která je uložena v balíku student.
Jednotlivé parametry znamenají následující:
g - výraz reprezentující daný integrál ve tvaru Int(f(x), x)
u - součást integrandu, která se bude derivovat (viz výše uvedený vzorec)
Příkaz voláme
student[intparts](g,u); nebo with(student):
intparts(g,u);
2.1 Příklad 1.
Vypočtěte integrál 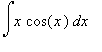 použitím metody per-partes.
použitím metody per-partes.
Řešení: Položme u = x, u' = 1, v' = cos(x), v = sin(x). Pak dostáváme:
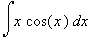 =
= 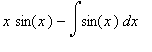 =
= ![]()
> with(student):
> vyr:=intparts(Int(x*cos(x), x), x);
![]()
Tento integrál dokážeme již vypočítat
> value(vyr);
![]()
>
2.2 Příklad 2.
Vypočtěte integrál 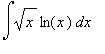 .
.
> vyr:=intparts(Int(sqrt(x)*ln(x),x), ln(x));
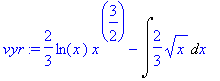
> value(vyr);
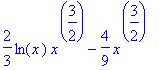
>
3. Integrace substitucí pro neurčitý integrál
Pro substituci se v Maplu užívá příkazu changevar .
student[changevar] (f, v) ; nebo with(student):
changevar(f, v); kde f je vyjádření substituce f(x) = g(t) ,
v výraz typu Int(f(x),x ) nebo changevar(f, v, t); kde t je nová integrační proměnná
3.1 Příklad 1.
mws verzeMějme vypočítat pomocí substituce integrál : 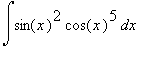
Řešení:
> with(student):
Při výpočtu použijeme substituci t = sin(x), dt = cos(x)dx
> expr:=changevar(sin(x)=t, Int((sin(x)^2*cos(x)^5),x), t);
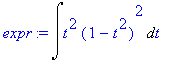
Spočítání integrálu:
> expr1:=value(expr);
![]()
Návrat k původní proměnné x:
> changevar(t=sin(x), expr1, x);
![]()
>
Řadu úloh lze řešit kombinací obou integračních metod.
3.2 Příklad 2.
Vypočtěte 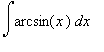 .
.
Řešení: Položme u = arcsin(x), u' = 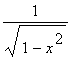 , v' = 1, v' = x.
, v' = 1, v' = x.
> expr:=intparts(Int(arcsin(x),x), arcsin(x));
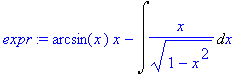
> expr1:=changevar(1-x^2=t,expr,t);
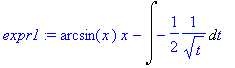
> expr2:=value(expr1);
![]()
> changevar(t=1-x^2, expr2, x);
![]()
>
4. Rozklad na parciální zlomky
Ryzí racionální funkci ![f(x) = P[n]/Q[m]](images/index46.gif) , kde n<m lze rozložit na součet parcialních zlomků takto.
, kde n<m lze rozložit na součet parcialních zlomků takto.
Nejdříve rozložíme polynom ve jmenovateli
![Q[m] = a[m]*(x-x[1])^k[1]*(x-x[2])^k[2]](images/index47.gif) ...
...
![(x-x[r])^k[r]*(x^2+p[1]*x+q[1])^l[1]*(x^2+p[2]*x+q[...](images/index48.gif) ...
... ![(x^2+p[s]*x+q[s])^l[s]](images/index49.gif)
kde ![]() je koeficient u nejvyšší
mocniny
je koeficient u nejvyšší
mocniny
![]() jsou reálné kořeny polynomu
jsou reálné kořeny polynomu ![]() , i = 1,2,...r o násobnostech
, i = 1,2,...r o násobnostech ![]()
![x^2+p[i]*x+q[i]](images/index54.gif) jsou kvadratické výrazy se
zápornými diskriminanty (i = 1,2,...s).
jsou kvadratické výrazy se
zápornými diskriminanty (i = 1,2,...s).
Potom pro f(x) jednoznačně platí, že
f(x) = ![]() =
= ![A[1]/(x-x[1])+A[2]/((x-x[1])^2)](images/index56.gif) + ... +
+ ... + ![A[k[1]]/((x-x[1])^k[1])](images/index57.gif) +
+
![B[1]/(x-x[2])+B[2]/((x-x[2])^2)](images/index58.gif) + ... +
+ ... + ![B[k[2]]/((x-x[2])^k[2])](images/index59.gif) + ...
+ ...
+ ![(K[1]*x+L[1])/(x^2+p[1]*x+q[1])+(K[2]*x+L[2])/((x^2...](images/index60.gif) + ... +
+ ... + ![(K[l[1]]*x+L[l[1]])/((x^2+p[1]*x+q[1])^l[1])](images/index61.gif) +
+
![(M[1]*x+N[1])/(x^2+p[2]*x+q[2])](images/index62.gif) +
+ ![(M[2]*x+N[2])/((x^2+p[2]*x+q[2])^2)](images/index63.gif)
+ ... + ![(M[l[2]]*x+N[l[2]])/((x^2+p[2]*x+q[2])^l[2])](images/index64.gif) + ...
+ ...
Maple provede rozklad na součet parciálních zlomku příkazem
> convert(f,parfrac,promenna);
![]()
kde f je racionální funkce
4.1 Příklad 1.
mws verzeVypočtěte integrál 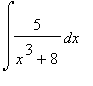
Rozložíme integrovanou funkci na součet parciálních zlomků:
> convert(5/(x^3+8),parfrac,x);
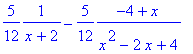
> int(%,x);
![]()
Tento integrál lze vypočítat také přímo
> Int(5/(x^3+8),x)=int(5/(x^3+8),x);
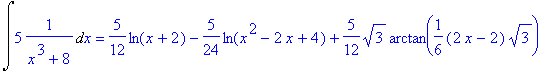
>
4.2 Příklad 2.
mws verzeVypočtěte 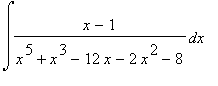
> convert((x-1)/(x^5+x^3-12*x-2*x^2-8),parfrac,x);
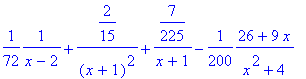
> int(%,x);
![]()
Můžeme spočítat i přímo:
> Int((x-1)/(x^5+x^3-12*x-2*x^2-8),x)=int((x-1)/(x^5+x^3-12*x-2*x^2-8),x);
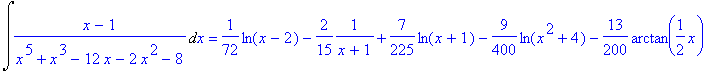
>
5. Určitý integrál - úvod
S ymbol 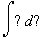 se nazývá integrač ní znak a vznikl
historicky nesprávným psaním součtového znaku
se nazývá integrač ní znak a vznikl
historicky nesprávným psaním součtového znaku ![]() . Riemannův
integrál je totiž definován pomocí
. Riemannův
integrál je totiž definován pomocí
tzv. horních a dolních součtů. Podrobnosti a také teoretickou podstatu problematiky lze nalézt v každé základní učebnici matematiky.
Pro ilustraci uvádíme několik názorných obrázků - pomocí procedur lowbox a upbox.
5.1 Animace pomoci upbox
mws verze> restart;with(plots):
Warning, the name changecoords has been redefined
Nejdříve musíme proceduru upbox nadefinovat:
> upbox:=proc(f,a,b,n)
local a1, b1, k, x, i, j, J, halt, critpt, critset, M, A, B, C;
global upsum;
with(plottools):
a1:=evalf(a):b1:=evalf(b): k:=(b1-a1)/n; for i from 0 to n do
x[i]:=a1+i*k:od: critpt:=[];halt:=1;
while halt=1 do if
type(fsolve(D(f)(x),x,avoid={seq(x=critpt[i],i=1..nops(critpt))},x=a1..b1),numeric)=true
then
critpt:=sort([op(critpt),fsolve(D(f)(x),x,avoid={seq(x=critpt[i],i=1..nops(critpt))},x=a1..b1)]);
else critpt; halt:=0;
fi;
od;for i from 1 to n do
critset[i]:={x[i-1],x[i]};
for j in critpt do
if x[i-1]< j and j < x[i]
then critset[i]:={op(critset[i]),j};
else fi; M[i]:=max(op(map(f,critset[i])));
od; B[i]:=POLYGONS([[x[i-1],0],[x[i-1],M[i]],[x[i],M[i]],[x[i],0]]);
od:
C:=PLOT(seq(B[i],i=1..n),COLOR(RGB,0,.8,.2)):
A:=plot(f(x),x=a1..b1,scaling=constrained,colour=red,thickness=2):
plots[display]({A,C});end:
Význam parametrů procedury:
f.........funkce, kterou integrujeme;
a, b....hranice intervalu;
n........počet pravidelných částí, na které interval dělíme (počet obdélníků);
> f:=x->sin(x^2);a:=0;b:=sqrt(2*Pi);n:=10;
![]()
![]()
![]()
![]()
Vykresleni jednoho grafu:
> upbox(f,a,b,n);
Warning, the name arrow has been redefined
![[Maple Plot]](images/index80.gif)
Animaci vytvoříme takto:
> L:=[5, 10, 20,40,60,80,100]:
> for i in L do
UB[i]:=upbox(f,a,b,i):
od:
plots[display]([seq(UB[i],i=L)],insequence=true,scaling=constrained);
![[Maple Plot]](images/index81.gif)
Totožně můžeme pracovat také s dolními součty:
> restart;with(plots):
Warning, the name changecoords has been redefined
Nadefinování:
> lowbox:=proc(f,a,b,n)
local a1, b1, k, x, i, j, J, halt, critpt, critset, m, A, B, C;
global lowsum;
with(plottools):
a1:=evalf(a):b1:=evalf(b):
k:=(b1-a1)/n;
for i from 0 to n do
x[i]:=a1+i*k:od:
critpt:=[];halt:=1;
while halt=1 do if
type(fsolve(D(f)(x),x,avoid={seq(x=critpt[i],i=1..nops(critpt))},x=a1..b1),numeric)=true
then
critpt:=sort([op(critpt),fsolve(D(f)(x),x,avoid={seq(x=critpt[i],i=1..nops(critpt))},x=a1..b1)]);
else critpt; halt:=0;
fi;
od;
for i from 1 to n do
critset[i]:={x[i-1],x[i]};
for j in critpt do
if x[i-1]< j and j < x[i]
then critset[i]:={op(critset[i]),j};
else fi;
m[i]:=min(op(map(f,critset[i])));
od;
B[i]:=POLYGONS([[x[i-1],0],[x[i-1],m[i]],[x[i],m[i]],[x[i],0]]);
od:
C:=PLOT(seq(B[i],i=1..n),COLOR(RGB,0,.8,.2)):
A:=plot(f(x),x=a1..b1,scaling=constrained,colour=red,thickness=2):
plots[display]({A,C});
end:
Nastavení:
> f:=x->sin(x^2):a:=0:b:=sqrt(2*Pi):n:=10:
Vykreslení:
> lowbox(f,a,b,n);
Warning, the name arrow has been redefined
![[Maple Plot]](images/index82.gif)
Animace:
> L:=[5, 10, 20,40,60,80,100]:
> for i in L do
LB[i]:=lowbox(f,a,b,i):
od:
plots[display]([seq(LB[i],i=L)],insequence=true,scaling=constrained);
![[Maple Plot]](images/index83.gif)
>
Dále se zaměříme na výpočet určitého integrálu.
Příkaz, který vypočítá určitý integrál, má v Maple tvar:
int (výraz,x = a..b);
kde výraz je integrovaná funkce, x je integrační proměnná
a - dolní mez , b - horní mez
Pro výpis neurčitého integrálu se používá příkaz Int (výraz, x=a..b) .
5.3 Příklad 1.
Vypočítejte 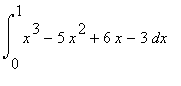 .
.
> restart;
> plot(x^3-5*x^2+6*x-3,x=0..1,scaling=constrained);
![[Maple Plot]](images/index85.gif)
> int(x^3-5*x^2+6*x-3,x=0..1);
![]()
Velmi výhodné je uvědomit si dvě ze základních vlastnotí určitého integrálu - pro případ mezí symetrických vzhledem k počátku
souřadného systému tj. interval <-a,a>, zejména pro "ruční " počítání.
Platí . a) 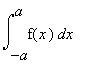 =
0, pro funkci lichou
=
0, pro funkci lichou
b) 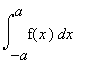 =
= 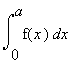 , pro funkci sudou
, pro funkci sudou
Ukažme na příkladu :
5.4 Příklad 2.
Vypočítejte 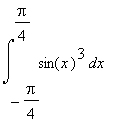
> Int(sin(x)^3,x=-Pi/4..Pi/4)=int(sin(x)^3,x=-Pi/4..Pi/4);
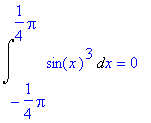
> plot(sin(x)^3,x=-Pi/4..Pi/4,filled=true,color=yellow);
![[Maple Plot]](images/index92.gif)
> Int(sin(x)^2,x=-Pi/4..Pi/4)=int(sin(x)^2,x=-Pi/4..Pi/4);
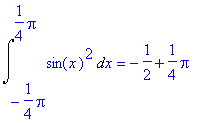
> plot(sin(x)^2,x=-Pi/4..Pi/4,filled=true,color=blue);
![[Maple Plot]](images/index94.gif)
>
6. Metoda per partes pro určitý integrál
Vypočítejte 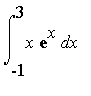 .
.
> plot(x*exp(x),x=-1..3,color=red);
![[Maple Plot]](images/index96.gif)
Necht´ u = x a tedy v´= ![]() , pak u´= 1 a v=
, pak u´= 1 a v= ![]() .
.
> Int(x*exp(x),x=-1..3)=student[intparts](Int(x*exp(x),x=-1..3),x);
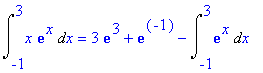
> value(rhs(%));
![]()
>
7. Substituční metoda pro určitý integrál
Vypočítejte 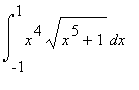 .
.
> plot(x^4*sqrt(x^5+1),x=-1..1,color=black,style=point,scaling=constrained);
![[Maple Plot]](images/index102.gif)
> I1:=Int(x^4*sqrt(x^5+1),x=-1..1);
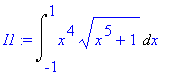
Použijeme substituci 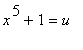 .
.
student[changevar](x^5+1=u,I1,u);
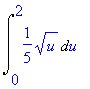
> value(%);
>
![]()
>
8.1 Příklad 1.
mws verzeVypočítejte 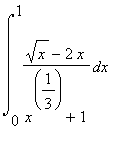 .
.
> plot((sqrt(x)-2*x)/(x^(1/3)+1),x=0..1,color=black,style=line);
![[Maple Plot]](images/index108.gif)
> int((sqrt(x)-2*x)/(x^(1/3)+1),x=0..1);
![]()
lze zadat výpočet pomocí substituce
> with(student):
> changevar(x^(1/6)=t,Int((sqrt(x)-2*x)/(x^(1/3)+1),x=0..1),t);
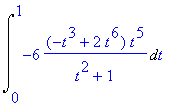
> value(%);
![]()
>
8.2 Příklad 2.
mws verzeVypočítejte 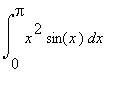 .
.
> plot(x^2*sin(x),x=0..Pi,color=blue);
![[Maple Plot]](images/index113.gif)
Necht´ u = ![]() a v' = sin(x)
a v' = sin(x)
> student[intparts](Int(x^2*sin(x),x=0..Pi),x^2);
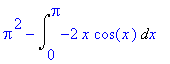
Metodu per partes použijeme ještě jednou, za funkci, kterou budeme derivovat, volíme opět polynom
> student[intparts](%,x);
>
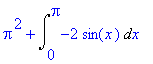
> value(%);
![]()
>
8.3 Příklad 3.
mws verzeVypočítejte 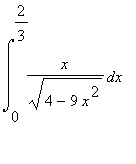 .
.
> plot(x/sqrt(4-9*x^2),x=0..2/3,color=orange);
![[Maple Plot]](images/index119.gif)
> I2 := Int(x/sqrt(4-9*x^2),x=0..2/3);
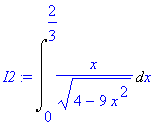
Substituce 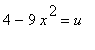
> student[changevar](4-9*x^2=u,I2,u);
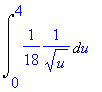
Výraz zjednodušíme pomocí příkazu simplify.
> simplify(%);
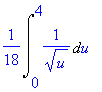
> value(%);
![]()
>
8.4 Příklad 4.
mws verzeVypočítejte 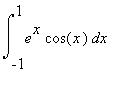 .
.
> plot(exp(x)*cos(x),x=-1..1,color=cyan,style=point,scaling=constrained);
![[Maple Plot]](images/index126.gif)
Zde je jedno, kterou funkci budeme považovat za u a
kterou za v'. Položme tedy u= ![]() a v'=cos x.
a v'=cos x.
> I1 := Int(exp(x)*cos(x),x=0..Pi/2);
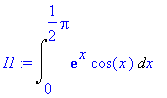
Použijeme metodu per-partes.
Nechť u = ![]() a v´=
a v´= ![]() .
.
> with(student):
> student[intparts](I1,exp(x));
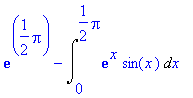
>
Nyní nastala situace, kdy vzniklý integrál není
o nic jednodušší, než integrál původní. Opět použijeme metodu per-partes a to
užitím u= ![]() .
.
> student[intparts](%,exp(x));
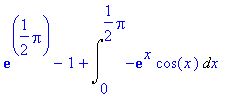
>
Pokud z integrálu vytkneme -1, vzniklý integrál je úplně shodný s původně zadaným.
> isolate(I1=expand(%),I1);
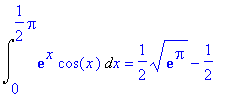
Nyní ukážeme, že Maple umí spočítat tento integrál přímo, předcházející výpočty popisují "ruční" výpočet
> Int(exp(x)*cos(x),x=0..Pi/2)=int(exp(x)*cos(x),x=0..Pi/2);
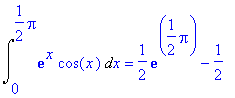
>
8.5 Příklad 5.
mws verzeVypočítejte 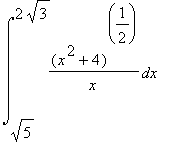 .
.
> Int(sqrt(x^2+4)/x,x=sqrt(5)..sqrt(12));
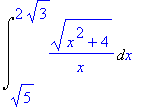
> plot(sqrt(x^2+4)/x,x=sqrt(5)..sqrt(12));
![[Maple Plot]](images/index138.gif)
Substituce 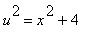 .
.
> changevar(x^2+4=u^2,Int(sqrt(x^2+4)/x,x=sqrt(5)..sqrt(12)),u);
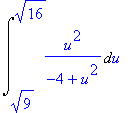
> value(%);
![]()
> combine(%);
![]()
Při "ručním" výpočtu je nutno využít rozklad na parciální zlomky.
> convert(u^2/(u^2-4),parfrac,u);
![]()
> int(%,u=3..4);
![]()
> combine(%);
![]()
>
8.6 Příklad 6.
Vypočítejte 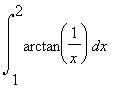 .
.
> In:=Int(arctan(1/x),x=1..2);
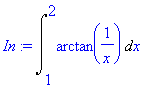
> plot(arctan(1/x),x=-1..2,color=black);
>
![[Maple Plot]](images/index148.gif)
Metoda per-partes u = 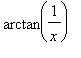 .
.
>
> student[intparts](In,arctan(1/x));
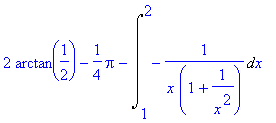
> simplify(%);
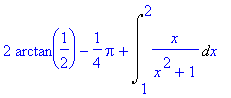
> value(%);
![]()
> combine(%);
![]()
>
8.7 Příklad 7.
mws verzeVypočteme integrál 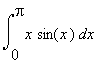 .
.
Řešení: Položme u = x, u' = 1, v' = sin(x), v = -cos(x).
> with(student):
> cv:=intparts(Int(x*sin(x),x=0..Pi), x);
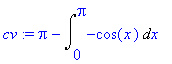
> value(cv);
![]()
>
8.8 Příklad 8.
mws verzeVypočteme integrál 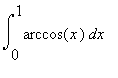 .
.
Řešení: Nejprve použijeme metodu per partes
u = arccos(x), u' = 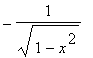 , v' = 1, v = x.
, v' = 1, v = x.
> vyr:=intparts(Int(arccos(x),x=0..1), arccos(x));
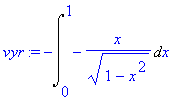
Nyní použijeme metodu substituce
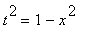 ,
, ![]() .
.
> vyr1:=changevar(1-x^2=t^2, vyr, t);
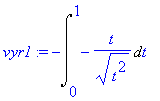
> value(vyr1);
![]()
>
8.9 Příklad 9.
mws verzeVypočteme integrál 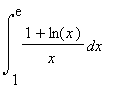 .
.
Řešení: pomocí metody substituce ln(x) = t.
Při metodě substituce u určitého integrálu je
nutné přepočítat meze integrálu: ![]() = ln(1) = 0,
= ln(1) = 0, ![]() = ln(e)=1.
= ln(e)=1.
> with(student):
> integral:=changevar(ln(x)=t, Int((1+ln(x))/x, x=1..exp(1)), t);
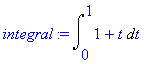
A tento integrál již lze jednoduše spočítat.
> value(integral);
![]()
>
9. Užití integrálního počtu
9.1 Obsahy rovinných obrazců
9.1.1 Příklad 1.
mws verzeVypočteme obsah plochy omezené osou x a grafem
funkce f(x) = sin(x) na intervalu <0, ![]() >.
>.
Řešení:
> with(plots):
Warning, the name changecoords has been redefined
> p1:=plot(sin(x),x=0..Pi,filled = true , color=gray):
> p2:=plot(sin(x),x=-2..2*Pi, color=red):
> display({p1,p2});
![[Maple Plot]](images/index170.gif)
> Int(sin(x),x=0..Pi):%=value(%);
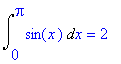
>
9.1.2 Příklad 2.
mws verzeVypočteme obsah plochy omezené grafy funkcí f(x)
= ![]() , g(x) =
, g(x) = ![]() .
.
Řešení:
> with(plots):
> p1:=plot(sqrt(x), x=0..3, y=0..3):
> p2:=plot(x^2, x=0..3):
> display({p1,p2});
![[Maple Plot]](images/index174.gif)
Nerovnost 0 <= ![]() <=
<= ![]() platí na intervalu <0,1>.
platí na intervalu <0,1>.
> Int(sqrt(x)-x^2,x=0..1):%=value(%);
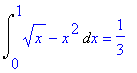
>
9.1.3 Příklad 3.
mws verzeVypočteme obsah plochy omezené grafem funkce f(x)
= 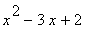 a osou x na intervalu <0,3>.
a osou x na intervalu <0,3>.
Řešení:
Je-li f(x) spojitá funkce nabývající na intervalu <a,b> záporných hodnot, pak obsah plochy omezené grafem této funkce a osou x na intervalu <a,b> určíme tak, že vypočteme obsah plochy omezené grafem funkce -f(x) na intervalu <a,b>.
> with(plots):
> p1:=plot(sin((1/2*x-1.5)^3)+2,x=1..5,y=0..4, filled=true, color=gray):
> p2:=plot(0,x=0..6,y=-1..4):
> p3:=textplot([[1,-0.8,`a`],[5,-0.8,`b`],[3,2.3,`-f(x)`]] ,align={ABOVE,RIGHT}):
> p4:=plot(0,x=0..6,y=-4..1):
> p5:=plot(-sin((1/2*x-1.5)^3)-2,x=1..5,y=-4..1, filled=true, color=gray):
> p6:=textplot([[1,0.7,`a`],[5,0.7,`b`],[3,-2.4,`f(x)`]] ,align={ABOVE,RIGHT}):
> p7:=plot(sin((1/2*x-1.5)^3)+2,x=1..5,y=0..4,color=black, thickness=2):
> p8:=plot(-sin((1/2*x-1.5)^3)-2,x=1..5,y=-4..0,color=black, thickness=2):
> display({p5,p4,p6,p8});
display({p1,p2,p3,p7});
![[Maple Plot]](images/index179.gif)
![[Maple Plot]](images/index180.gif)
Nyní nakreslíme danou funkci
> p1:=plot(x^2-3*x+2,x=0..3,filled=true, color=yellow):
> p2:=plot(x^2-3*x+2,x=0..3, thickness=2, color=black):
> display({p1,p2});
![[Maple Plot]](images/index181.gif)
> Int(x^2-3*x+2, x=0..1)+Int(-x^2+3*x-2, x=1..2)+Int(x^2-3*x+2, x=2..3):%=value(%);
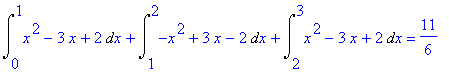
>
9.1.4 Příklad 4.
mws verzeVypočítejte obsah množiny ohraničené křivkami 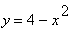 ,
, ![]() .
.
Pomocí Maple V si nadefinujeme funkce
> f := x -> 4 - x^2; g := x ->1-2*x;
![]()
![]()
Vypočítáme jejich průsečíky
> solve({y=f(x),y=g(x)},{x,y});
![]()
> solve({f(x)=0},{x});
![]()
> solve({g(x)=0},{x});
![]()
Nyní tyto dvě funkce necháme vykreslit pomocí příkazu plot , na intervalu ohraničeném body průniku
> Plt1 := plot({4-x^2,1-2*x},x=-1..3,color=black):plots[display](Plt1,style=line,font=[TIMES,ROMAN,11]);
![[Maple Plot]](images/index190.gif)
Obsah plochy vypočítáme jako integrál z rozdílu funkcí f(x) a g(x) na intervalu ohraničeném body průniku.
> Int(f(x)-g(x),x=-1..3)=int(f(x)-g(x),x=-1..3);
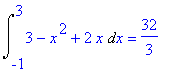
>
9.1.5 Příklad 5.
mws verzeVypočítejte obsah množiny ohraničené křivkami 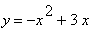 a
a 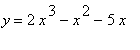 .
.
Nyní si funkce nadefinujeme
> f1 := x -> -x^2+3*x; f2 := x -> 2*x^3-x^2-5*x;
![]()
![]()
> solve(f1(x)=f2(x),{x});
![]()
> solve({-x^2+3*x=0},{x});
![]()
> solve({2*x^3-x^2-5*x=0},{x});
![]()
Nyní si nakresleme grafy těchto funkcí:
> plot({f1,f2},-2..2,color=black,style=line,font=[TIMES,ROMAN,11]);
![[Maple Plot]](images/index199.gif)
Obsah dané množiny se tedy skládá ze dvou částí, na intervalu [-2,0] platí f2(x) >= f1(x) a na intervalu [0,2] platí f1(x) >= f2(x). Budeme proto počítat dva integrály. Ukažme dvě možnosti výpočtu:
> Int(f2(x)-(f1(x)),x=-2..0)+Int(f1(x)-f2(x),x=0..2):%= value(%);
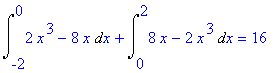
> Plocha:=Int(f2(x)-(f(x)),x=-2..0)+Int(f1(x)-f2(x),x=0..2)=int(2*x^3-8*x,x = -2 .. 0)+int(8*x-2*x^3,x = 0 .. 2);
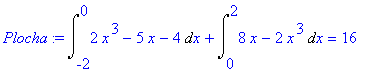
>
9.1.6 Příklad 6.
mws verzeVypočítejte obsah množiny ohraničené křivkami ![]() ,
, ![]() ,
, ![]() a
a 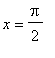 .
.
nadefinujeme funkce sinus a kosinus
> f1 := x -> sin(x); f2 := x -> cos(x);
![]()
![]()
> solve(f1(x)=f2(x),x);
![]()
Nyní si funkce necháme na příslušném intervalu vykreslit, tedy na intervalu [0,Pi/2]
> plot({sin(x),cos(x)},x=0..Pi/2,color=black,style=line,font=[TIMES,ROMAN,11],scaling=constrained);
![[Maple Plot]](images/index209.gif)
Na intervalu [0,Pi/4] platí sin(x) >= cos(x) a na intervalu [Pi/4,Pi/2] cos(x) >= sin(x). Budeme počítat součet dvou příslušných integrálů.
> PL1:=Int(f2(x)-f1(x),x=0..Pi/4)+Int(f1(x)-f2(x),x=Pi/4..Pi/2)=int(f2(x)-f1(x),x=0..Pi/4)+int(f1(x)-f2(x),x=Pi/4..Pi/2);
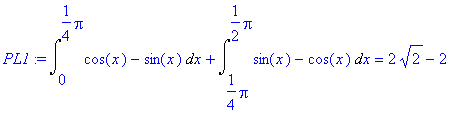
>
9.1.7 Poznámka
mws verzePro větší názornost vymezení plochy obrazce mezi dvěma křivkami v rovině můžeme použít tuto proceduru:
> restart;
> plocha:=proc(f::anything,g::anything)
> local p,q1,q2,s,a,r,t,b,c,i;
> a:={};
> t:=0.;
> s:=[];
> while type(t,'float')=true do
> t:=fsolve(f=g,x,avoid=a,maxsols=1);
> if type(t,'float')=true then
> s:=[seq(s[i],i=1..nops(s)),t];
> a:=a union {x=t};
> end if;
> end do;
> s:=sort(s);
> b:=s[1];
> c:=s[nops(s)];
> t:=0.;
> a:={seq(x=s[i],i=1..nops(s))};
> while type(t,'float')=true do
> t:=fsolve(f,x=b..c,avoid=a,maxsols=1);
> if type(t,'float')=true then
> s:=[seq(s[i],i=1..nops(s)),t];
> a:=a union {x=t};
> end if;
> end do;
> t:=0.;
> a:={seq(x=s[i],i=1..nops(s))};
> while type(t,'float')=true do
> t:=fsolve(g,x=b..c,avoid=a,maxsols=1);
> if type(t,'float')=true then
> s:=[seq(s[i],i=1..nops(s)),t];
> a:=a union {x=t};
> end if;
> end do;
> s:=sort(s);
> b:=s[1];
> c:=s[nops(s)];
> p:=[plot(f,x=b..c,thickness=2,color=black),plot(g,x=b..c,thickness=2,color=black)];
> for i from 1 to nops(s)-1 do
> if (evalf(subs(x=(s[i]+s[i+1])/2,f))>=0) and (evalf(subs(x=(s[i]+s[i+1])/2,g))>=0) then
> if (evalf(subs(x=(s[i]+s[i+1])/2,f))>evalf(subs(x=(s[i]+s[i+1])/2,g))) then
> q1:=plot(g,x=s[i]..s[i+1],filled=true,color=white);
> q2:=plot(f,x=s[i]..s[i+1],filled=true,color=red);
> else q1:=plot(f,x=s[i]..s[i+1],filled=true,color=white);
> q2:=plot(g,x=s[i]..s[i+1],filled=true,color=red);
> end if;
> elif (evalf(subs(x=(s[i]+s[i+1])/2,f))<=0) and (evalf(subs(x=(s[i]+s[i+1])/2,g))<=0) then
> if (evalf(subs(x=(s[i]+s[i+1])/2,f))>evalf(subs(x=(s[i]+s[i+1])/2,g))) then
> q1:=plot(f,x=s[i]..s[i+1],filled=true,color=white);
> q2:=plot(g,x=s[i]..s[i+1],filled=true,color=red);
> else
> q1:=plot(g,x=s[i]..s[i+1],filled=true,color=white);
> q2:=plot(f,x=s[i]..s[i+1],filled=true,color=red);
> end if;
> else
> q1:=plot(f,x=s[i]..s[i+1],filled=true,color=red);
> q2:=plot(g,x=s[i]..s[i+1],filled=true,color=red);
> end if;
> p:=[seq(p[i],i=1..nops(p)),q1,q2];
> end do;
> plots[display](p);
> end proc;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> plocha(sin(x),x^2);
![[Maple Plot]](images/index255.gif)
> plocha((x^2-1)*(x^2-4),sin(x));
![[Maple Plot]](images/index256.gif)
9.1.8 Příklad 7.
mws verzeVypočteme obsah rovinného obrazce omezeného
křivkou vyjádřené parametrickýmo rovnicemi x = a(t-sin(t)) , y = a(1-cos(t)) , t leží ![]() , a>0.
, a>0.
Řešení:
Obsah rovinného obrazce omezeného obloukem čáry
vyjádřené parametrickými rovnicemi ![]() s mezemi
parametru
s mezemi
parametru ![]() (
( ![]() ) je vyjádřen
vztahem
) je vyjádřen
vztahem
![S = Int(psi(t)*abs(diff(phi(t),t)),t = t[1] .. t[2]...](images/index261.gif)
Nakreslíme danou funkci
> with(plots):
> p1:=plot([t-sin(t), 1-cos(t), t=0..2*Pi], scaling=constrained, thickness=3, color=black):
> p2:=plot([t-sin(t), 1-cos(t), t=0..2*Pi], scaling=constrained, color=gray, filled=true):
> display({p1,p2});
![[Maple Plot]](images/index262.gif)
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
nyní dosadíme do vzorce:
> Int(a*(1-cos(t))*Diff(a*(t-sin(t)),t), t=0..2*Pi):%=value(%);
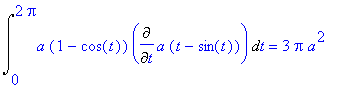
>
9.2 Objem rotačního tělesa
A. Objem tělesa vzniklého rotací křivky, ohraničeného obloukem čáry y = f(x), osou x a přímkami x = a, x = b, a < b, kolem osy x je
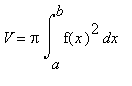
B. Objem tělesa vzniklého rotací křivky, ohraničeného obloukem čáry y = f(x), osou y a přímkami y = a, y = b, a < b, kolem osy y je
. 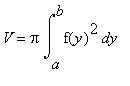 .
.
>
Ukažme pro ilustraci několik obrázků těles, která vznikají rotací dané křivky
> with(plots):
> tubeplot([t,0,0],t=0..Pi,radius=sin(t),tubepoints=20);
Můžeme také využít krátké procedury, která animací ukazuje rotaci křivky při vzniku rotačního tělesa:
![[Maple Plot]](images/index271.gif)
> rotate3d:=proc(f::anything,xrange::equation,yrange::equation)
> local t;
> return(plots[animate3d]([x,f(x)*cos(t),f(x)*sin(t)],xrange,yrange,t=0..2*Pi,orientation=[-100,60],axes=normal));
> end proc;
![]()
![]()
![]()
![]()
> rotate3d(sin(x),x=0..Pi,y=-1..1);
![[Maple Plot]](images/index276.gif)
> rotate3d(x^2,x=-1..1,y=0..1);
![[Maple Plot]](images/index277.gif)
> rotate3d(exp(-x^2),x=-1..1,y=0..1);
![[Maple Plot]](images/index278.gif)
9.2.1 Příklad 1.
mws verzeVypočítáme objem tělesa vzniklého rotací
rovinného obrazce ohraničeného křivkami 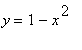 ,
, 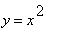 , kolem osy x.
, kolem osy x.
Řešení:
> p1:=plot(1-x^2, x=-1.5..1.5, y=-1.5..1.5):
> p2:=plot(x^2, x=-1..1):
> p3:=textplot([[-1.3,-1,`1-x^2`],[-1.2,0.8,`x^2`]] ,align={ABOVE,RIGHT}):
> display({p1,p2,p3});
![[Maple Plot]](images/index281.gif)
Nejprve stanovíme meze, jako průsečíky grafů obou křivek:
> solve(1-x^2=x^2,x);
![]()
Objem tělesa ![]() , kde
, kde ![]() je objem tělesa vytvořený rotací křivky
je objem tělesa vytvořený rotací křivky 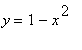 v mezích
v mezích 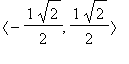 a osou x,
a osou x, ![]() je objem tělesa vytvořený rotací křivky
je objem tělesa vytvořený rotací křivky 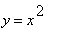 v mezích
v mezích 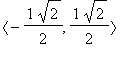 a osou x.
a osou x.
Objem tělesa tedy je:
> Pi*Int((1-x^2)^2-(x^2)^2,x=-1/2*sqrt(2)..1/2*sqrt(2)):%=value(%);
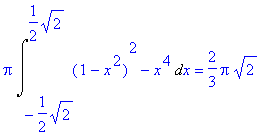
>
9.2.2 Příklad 2.
mws verzeVypočítáme objem tělesa vzniklého rotací
rovinného obrazce ohraničeného čarami 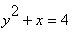 ,
, ![]() , kolem osy y.
, kolem osy y.
Řešení :
Meze stanovíme řešením rovnic obou čar: x = 0, 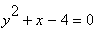 ,
,
> solve(0=y^2-4,y);
![]()
![]() vypočítáme z rovnice křivky:
vypočítáme z rovnice křivky: 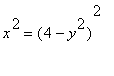
Dosazením do vzorce dostáváme objem:
> Pi*Int((4-y^2)^2,y=-2..2):%=value(%);
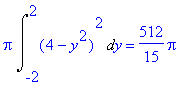
>
9.2.3 Příklad 3.
mws verzeJe-li funkce dána parametrickými rovnicemi
![]() ,
, ![]() , kde
, kde ![]()
![]()
![]() a
a ![]() je v tomto intervalu spojitá a
nezáporná, je objem rotačního tělesa při otáčení kolem osy x dán vzorcem
je v tomto intervalu spojitá a
nezáporná, je objem rotačního tělesa při otáčení kolem osy x dán vzorcem
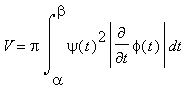
rotací kolem osy y 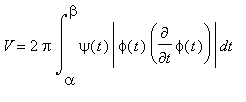
Vypočteme objem rotačního tělesa vzniklého rotací rovinného obrazce omezeného křivkou vyjádřené parametrickýmo rovnicemi x = a(t-sin(t)),
y = a(1-cos(t)), t leží ![]() , a>0, kolem osy x.
, a>0, kolem osy x.
Řešení :
x = a( t-sin(t)) = ![]()
y = a(1-cos(t)) = ![]()
>
> Diff(a*(t-sin(t)),t):%=value(%);
![]()
Dosazením do vzorce dostáváme:
> Pi*Int((a*(1-cos(t)))^2*a*(1-cos(t)), t=0..2*Pi):%=value(%);
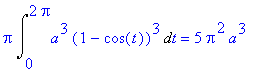
>
9.2.4 Příklad 4.
mws verzeUrčete objem rotačního tělesa vzniklého rotací
funkce ![]() kolem osy x na uzavřeném
intervalu (Pi/2,2Pi)
kolem osy x na uzavřeném
intervalu (Pi/2,2Pi)
> plot((sin(x)+cos(x))^2,x=Pi/2..2*Pi);
![[Maple Plot]](images/index312.gif)
> Pi*int((sin(x)+cos(x))^2,x=Pi/2..2*Pi);
![]()
> simplify(%);
![]()
>
9.3 Délka oblouku rovinné křivky
Délka oblouku L spojité rovinné křivky y = f(x) pro x leží <a,b>, která má v intervalu <a,b> spojitou derivaci, je dána vzorcem
V = 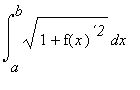
9.3.1 Příklad 1.
mws verzeVypočítáme délku křivky 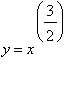 v intervalu <0,4>.
v intervalu <0,4>.
Řešení :
> plot(x^(3/2), x=0..4);
![[Maple Plot]](images/index317.gif)
V intervalu <0,4> má daná křivka spojitou derivaci
> `y'`= diff(x^(3/2),x);
![]()
Dosadíme do vzorce:
> Int(sqrt(1+(3/2*sqrt(x))^2),x=0..4):%=value(%);
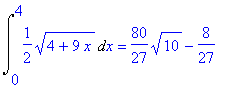
>
9.3.2 Příklad 2.
mws verzeVypočítejte délku grafu funkce ln(x) mezi body (
![]() ), (
), ( ![]() ).
).
Nejdříve si vypočítáme derivaci funkce ln(x)
> diff(log(x),x);
![]()
Délka křivky tedy je
> Int(sqrt(1+1/x^2),x=sqrt(3)..sqrt(8));
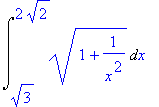
> simplify(%);
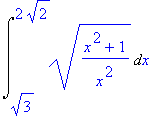
zvolíme substituce 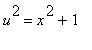
> student[changevar](u^2=x^2+1,%,u);
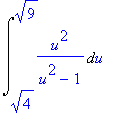
> simplify(%);
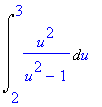
dále řešíme vzniklý integrál rozkladem na parciální zlomky
> convert(u^2/(u^2-1),parfrac,u);
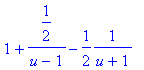
> int(%,u=2..3);
![]()
> combine(%);
![]()
>
Délka oblouku L spojité
rovinné křivky dané parametrickými rovnicemi ![]() ,
, ![]() , t leží v
, t leží v ![]() , mající spojité
derivace
, mající spojité
derivace ![]() ´(t),
´(t), ![]() ´(t) je dána
vzorcem:
´(t) je dána
vzorcem:
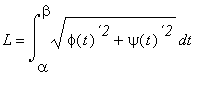
9.3.3 Příklad 3.
Vypočteme délku křivky danou parametrickými
rovnicemi 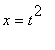 ,
, 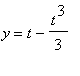 pro t z intervalu
pro t z intervalu ![]() .
.
Řešení :
> plot([t^2, t-t^3/3, t=0..sqrt(3)], scaling=constrained, thickness=3, color=black);
![[Maple Plot]](images/index340.gif)
V intervalu ![]() jsou
derivace
jsou
derivace ![]() ´(t),
´(t), ![]() ´(t) spojité,
dosadíme:
´(t) spojité,
dosadíme:
> `x'`=diff(t^2,t);
![]()
> `y'`=diff(t-t^3/3,t);
![]()
> Int(sqrt((2*t)^2+(1-t^2)^2),t=0..sqrt(3)):%=value(%);
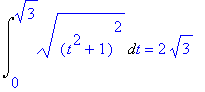
>
9.3.4 Příklad 4.
Vypočítejte délku křivky - asteroidy -
![]()
> plot([5*cos(t)^3,5*sin(t)^3,t=0..2*Pi],color=black,
> scaling=CONSTRAINED,font=[TIMES,ROMAN,11]);
![[Maple Plot]](images/index348.gif)
> diff(5*cos(t)^3,t)^2+diff(5*sin(t)^3,t)^2;
![]()
> delkakrivky:=int(sqrt(%),t=0..2*Pi);
![]()
> simplify(%);
![]()
>
9.4 Obsah rotační plochy (povrch tělesa)
Obsah rotační plochy, která vznikne rotací kolem osy x grafu spojité křivky y = f(x) v intervalu <a,b> a mající v tomto intervalu spojitou derivaci f '(x), je dán vzorcem:
![P = 2*Pi*Int(abs(f(x))*sqrt(1+[`f(x)'`]^2),x = a .....](images/index352.gif) .
.
Obsah rotační plochy , která vznikne rotací kolem osy x grafu
spojité křivky dané parametrickými rovnicemi ![]() ,
t leží v
,
t leží v ![]() , funkce
, funkce ![]() ´(t),
´(t), ![]() ´(t) jsou na tomto intervalu spojité,
přičemž funkce
´(t) jsou na tomto intervalu spojité,
přičemž funkce ![]() je ryze monotonní, je dán vzorcem:
je ryze monotonní, je dán vzorcem:
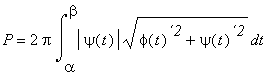
>
9.4.1 Příklad 1.
Vypočteme povrch koule o poloměru r oběma způsoby.
1. Z rovnice
kružnice 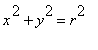 =>
=> 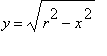 , x
leží <-r,r>. Rotace křivky kolem osy x.
, x
leží <-r,r>. Rotace křivky kolem osy x.
> with(plots):
> f:= x-> sqrt(r^2-x^2);
![]()
> plot(sqrt(1-x^2), x=-1..1, scaling=constrained);
![[Maple Plot]](images/index362.gif)
Dosazením do vzorce dostáváme:
> f := x -> sqrt(r^2-x^2);
![]()
> 2*Pi*Int(f(x)*sqrt(1+(diff(f(x),x))^2),x=-r..r):%=value(%);
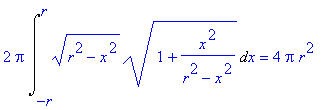
2 .
Parametrické vyjádření kružnice: x = ![]() (t) = rcos(t), y =
(t) = rcos(t), y = ![]() = rsin(t), t leží <0..
= rsin(t), t leží <0.. ![]() >.
>.
> Diff(phi,t) = diff(r*cos(t),t);
![]()
> Diff(psi,t) = diff(r*sin(t),t);
![]()
Dosadíme do vzorce:
> 2*Pi*Int(r*sin(t)*sqrt((-r*sin(t))^2+(r*cos(t))^2),t=0..Pi):%=value(%);
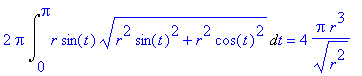
> combine(%);
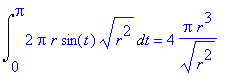
Maple uvažuje r jako konstantu o které neví , zda je kladná nebo záporná, proto neupraví odmocninu.
Můžeme upravit pomocí příkazu assume, kterým zadáme vlastnost r - poloměru.
> assume(r>0);
> 2*Pi*Int(r*sin(t)*sqrt((-r*sin(t))^2+(r*cos(t))^2),t=0..Pi):%=value(%);
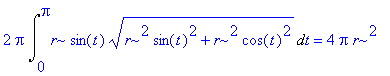
>
9.4.2 Příklad 2.
mws verzeVypočítejte délku křivky - asteroidy -
![]()
>
> plot([5*cos(t)^3,5*sin(t)^3,t=0..2*Pi],color=black,
> scaling=CONSTRAINED,font=[TIMES,ROMAN,11]);
![[Maple Plot]](images/index374.gif)
> diff(5*cos(t)^3,t)^2+diff(5*sin(t)^3,t)^2;
![]()
> delkakrivky:=int(sqrt(%),t=0..2*Pi);
![]()
> simplify(%);
![]()
>
9.5 Ukázky fyzikálních aplikací
9.5.1 Příklad 1.
mws verzeUrčete těžiště homogenní oblasti omezené
křivkami 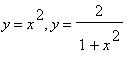
Nejdříve oblast omezenou křivkami nakreslíme
> restart;
> plot({x^2,2/(1+x^2)},x=-5..5,y=0..5,scaling=constrained);
![[Maple Plot]](images/index379.gif)
Nyní spočítáme průsečíky křivek, abychom měli meze integrálu
> y1:=x^2;
![]()
> y2:=2/(x^2+1);
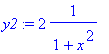
> solve(y1=y2,x);
![]()
Následuje výpočet statických momentů ![]()
![]() =
= 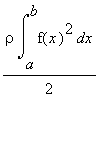
![S[y] = rho*Int(x*f(x),x = a .. b)](images/index386.gif)
Protože oblast je tvořena dvěma křivkami , statické momenty se budou odčítat.
> SX:=1/2*rho*Int(y2^2-y1^2,x=-1..1)=1/2*rho*int(y2^2-y1^2,x=-1..1);
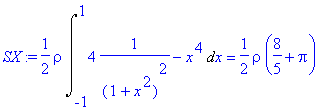
> SY:=rho*Int(x*(y2-y1),x=-1..1)=rho*int(x*(y2-y1),x=-1..1);
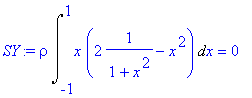
Výpočet hmotnosti ![]()
> m:=rho*Int(y2-y1,x=-1..1)=rho*int(y2-y1,x=-1..1);
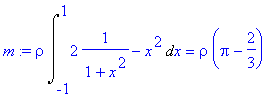
x - ová souřadnice těžiště ![x[T] = S[y]/m](images/index391.gif)
> Xt:=rhs(SY)/rhs(m);
![]()
> Xt := 0;
![]()
y - ová souřadnice těžiště ![y[T] = S[x]/m](images/index394.gif)
> Yt:=rhs(SX)/rhs(m);
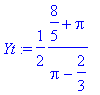
> Yt:=evala(Yt);
![]()
>
9.5.2 Příklad 2.
mws verze> restart;
Nalezněte souřadnice těžiště homogenního
drátu ve tvaru čtvrtkružnice o rovnici 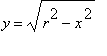 a
délce na ose x v intervalu
a
délce na ose x v intervalu
<-r/sqrt(2), r/sqrt(2)>.
Nejdříve si funkci nakreslíme. Pro kreslení
volíme ![]()
> plot(sqrt(9-x^2),x=-3/sqrt(2)..3/sqrt(2),y=0..3.3,scaling=constrained);
![[Maple Plot]](images/index399.gif)
Dále spočítáme statické momenty ![]() a hmotnost m .
a hmotnost m .
K tomu potřebujeme spočítat derivaci a 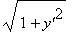
> dery:=Diff(sqrt(r^2-x^2),x)=diff(sqrt(r^2-x^2),x);
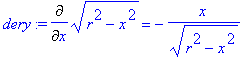
> odmoc:=sqrt(1+x^2/(r^2-x^2));
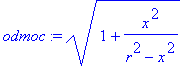
Statické momenty ![]() a
a ![]() jsou
jsou
![S[x] = rho*Int(f(x)*sqrt(1+f(x)^`´2`),x = a .. b)](images/index406.gif)
![S[y] = rho*Int(x*sqrt(1+f(x)^`'2`),x = a .. b)](images/index407.gif)
Nyní ubezpečíme počítač, že poloměr ![]() je vždy kladný příkazem
je vždy kladný příkazem ![]()
> assume(r>0);
> Sx:=rho*Int(sqrt(r^2-x^2)*odmoc,x=-r/sqrt(2)..r/sqrt(2))=rho*int(sqrt(r^2-x^2)*odmoc,x=-r/sqrt(2)..r/sqrt(2));
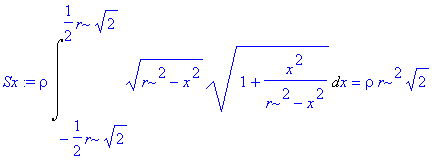
> Sy:=rho*Int(x*odmoc,x=-r/sqrt(2)..r/sqrt(2))=rho*int(x*odmoc,x=-r/sqrt(2)..r/sqrt(2));
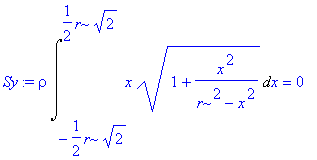
> m:=rho*Int(r/sqrt(r^2-x^2),x=-r/sqrt(2)..r/sqrt(2))=rho*int(r/sqrt(r^2-x^2),x=-r/sqrt(2)..r/sqrt(2));
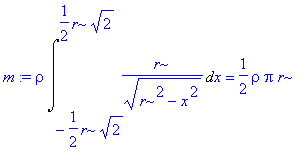
Souřadnice těžiště jsou :
x - ová souřadnice těžiště ![x[T] = S[y]/m](images/index413.gif)
> SX:=rhs(Sy)/rhs(m);
![]()
y - ová souřadnice těžiště ![y[T] = S[x]/m](images/index415.gif)
> SY:=rhs(Sx)/rhs(m);
![]()
>
9.5.3 Příklad 3.
mws verze> restart;
Určetě těžiště drátu (homogenního) ve tvaru jednoho oblouku cykloidy :
![]() , t
náleží do intervalu
, t
náleží do intervalu ![]() .
.
Nejprve křivku nakreslíme , ![]() .
.
> plot([t-sin(t),1-cos(t),t=0..2*Pi],scaling=constrained);
![[Maple Plot]](images/index420.gif)
Statické momenty ![]() se počítají dle vzorců :
se počítají dle vzorců : ![S[x] = rho*Int(psi(t)*sqrt(phi(t)^`´2`+psi(t)^`´2`)...](images/index422.gif)
![S[y] = rho*Int(phi(t)*sqrt(phi(t)^`´2`+psi(t)^`´2`)...](images/index423.gif)
> ffi:=a*(t-sin(t));
![]()
> ppsi:=a*(1-cos(t));
![]()
> derfi:=Diff(a*(t-sin(t)),t)=diff(a*(t-sin(t)),t);
![]()
> derpsi:=Diff(a*(1-cos(t)),t)=diff(a*(1-cos(t)),t);
![]()
> odmoc:=sqrt(rhs(derfi)^2+rhs(derpsi)^2);
![]()
> odmoc:=simplify(odmoc);
![]()
> odmoc:=expand(odmoc);
![]()
> SX:=rho*Int(ppsi*odmoc,t=0..2*Pi)=rho*int(ppsi*odmoc,t=0..2*Pi);
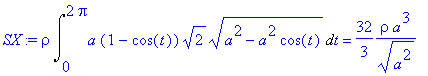
> SX := rho*Int(a*(1-cos(t))*sqrt(2)*sqrt(a^2-a^2*cos(t)),t = 0 .. 2*Pi) = 32/3*rho/(a^2)^(1/2)*a^3;
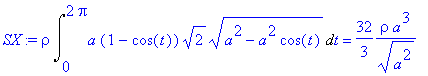
> assume(a>0);
> Sx:=simplify(rhs(SX));
![]()
Hmotnost se počítá podle vzorce ![m = Int(sqrt(phi(t)^`´2`+psi(t)^`´2`),t = t[1] .. t...](images/index434.gif)
> m:=Int(odmoc,t=0..2*Pi)=int(odmoc,t=0..2*Pi);
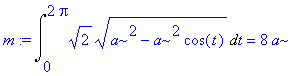
> x[t]:=Pi*a;
![]()
> y[t]:=Sx/rhs(m);
![]()
>
9.5.4 Příklad 4.
mws verze> restart;
Vypočítejte těžiště a momenty setrvačnosti
homogenního obrazce omezeného křivkami 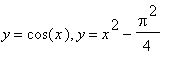
Nejdříve obrazec omezený křivkami nakreslíme
> plot({cos(x),x^2-Pi^2/4},x=-2..2);
![[Maple Plot]](images/index439.gif)
Z obrázku je vidět,že není potřeba počítat
průsečíky na ose x a že průsečíky jsou v bodech 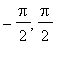
My je z cvičných důvodů spočítáme
> solve({y=cos(x),y=x^2-Pi^2/4},{x,y});
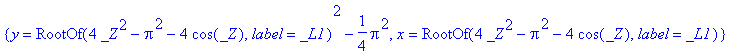
> evalf(%);
![]()
> fsolve({y=cos(x),y=x^2-Pi^2/4},{x,y},-2..2);
![]()
Jak je vidět Maple není všemocný a nejlepší řešení je vidět z obrázku
Nyní spočítáme statické momenty ![]() a hmotnost
a hmotnost ![]()
> vyr:=cos(x)^2-(x^2-Pi^2/4)^2;
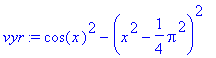
> Sx:=1/2*rho*Int(vyr,x=-Pi/2..Pi/2)=1/2*rho*int(vyr,x=-Pi/2..Pi/2);
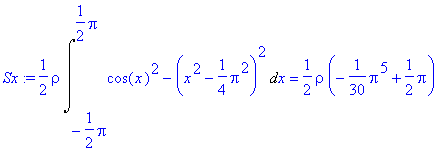
> SX:=rhs(%);
![]()
> vyr1:=x*(cos(x)-(x^2-Pi^2/4));
![]()
> vyr1 := x*(cos(x)-x^2+1/4*Pi^2);
![]()
> Sy:=rho*Int(vyr1,x=-Pi/2..Pi/2)=rho*int(vyr1,x=-Pi/2..Pi/2);
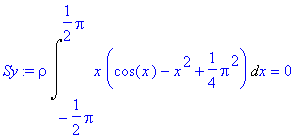
> SY:=rhs(%);
![]()
> vyr2:=cos(x)-(x^2-Pi^2/4);
![]()
> m:=rho*Int(vyr2,x=-Pi/2..Pi/2)=rho*int(vyr2,x=-Pi/2..Pi/2);
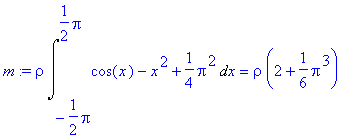
> mm:=rhs(%);
![]()
x - ová a y - ová souřadnice těžiště jsou
>
> xt:=SY/mm;
![]()
> yt:=SX/mm;
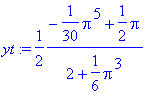
> yt:=evala(yt);
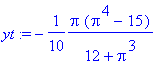
>
10. Nevlastní integrál
Připomeňme stručně, jak počítáme nevlastní integrál "ručně".Pro přímý výpočet uvažujeme limitu pro mez, která je buď nevlastní nebo je bodem nespojitosti
dané funkce ( v našem popisu např. horní mez ) :
> 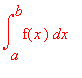 =
= 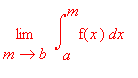 , obdobně zacházíme s nevlastním integrálem
vzhledem k dolní mezi.
, obdobně zacházíme s nevlastním integrálem
vzhledem k dolní mezi.
10.1 Příklad 1.
mws verzeVypočtěte objem tělesa vzniklého rotací
křivky y =  v intervalu (-
v intervalu (-
![]() ,
, ![]() ).
).
Je zřejmé, že výpočet objemu bude vlastně výpočet nevlastního integrálu.
Nakresleme si obrázek:
> plot(arctan(x)/sqrt(1+x^2),x=-infinity..infinity);

![]()
![]()
![[Maple Plot]](images/index467.gif)
> plot(arctan(x)/sqrt(1+x^2),x=-infinity..infinity,scaling=constrained);
![[Maple Plot]](images/index468.gif)
Tento obrázek neukazuje přesvědčivě, že křivka neprotíná osu x, ale zato nás jistě přesvědčí, že objem bude tvořen dvěma shodnými částmi.
Nakreslíme ještě jeden obrázek v bližším okolí počátku.
> plot(arctan(x)/sqrt(1+x^2),x=-20..20);
![[Maple Plot]](images/index469.gif)
Vyjádříme nyní objem pomocí známého vzorce :
V = ![]()
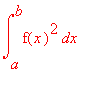 a objem vypočítáme, tedy
a objem vypočítáme, tedy
V = 2* ![]() *
* 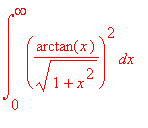
![]()
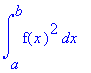
![]()
![]()
> V:=2*Pi*limit(int((arctan(x)/sqrt(1+x^2))^2,x=0..m), m=infinity);
![]()
V tomto případě jsme využili příkazů Maple pro výpočet limity a integrálu :
![]() = limit( f(x),x = r ); a
= limit( f(x),x = r ); a 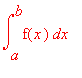 = int( f(x), x = a..b);
= int( f(x), x = a..b);
Pro "ruční" výpočet neurčitého
integrálu IN = 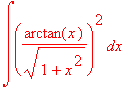 využíváme
obvykle substituci,
využíváme
obvykle substituci,
kterou můžeme také určit programu pro výpočet našeho integrálu - příkazem changevar
>
student[changevar] (f, v) ; nebo with(student):
changevar(f, v); kde f je vyjádření substituce f(x) = g(t) ,
v výraz Int(f(x),x = a..b)
nebo changevar(f, v, t); kde t je nová integrační proměnná
> student[changevar] (arctan(x)=t,Int((arctan(x)/sqrt(1+x^2))^2,x));
![]()
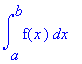
![]()
![]()
> value(%);
![]()
Napřed Maple dosadil substituci, dalším příkazem pak výpočet integrálu
> student[changevar] (arctan(x)=t,int((arctan(x)/sqrt(1+x^2))^2,x));
![]()
>
Tento příklad dosadí substituci a hned vypočte
> restart;
> with(student):
> changevar(arctan(x)=t,int((arctan(x)/sqrt(1+x^2))^2,x));
![]()
Nyní pokračujeme ve výpočtu určitého integrálu, protpže se jedná o integrál nevlastní - pomocí limity.
Napřed se vrátíme k původní proměnné.
> changevar(t=arctan(x),%);
![]()
> V=limit(%,x=infinity);
![]()
A toto byla další možnost
Maple ale umí vypočítat tento integrál přímo jako určitý s nevlastní mezí
> Int((arctan(x)/sqrt(1+x^2))^2,x=0..infinity)=int((arctan(x)/sqrt(1+x^2))^2,x=0..infinity);
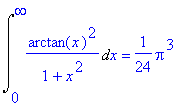
>
10.2 Příklad 2.
mws verzeUrčete plochu rovinného obrazce omezeného
křivkami y = 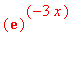 , y = 0 pro x
, y = 0 pro x ![]() <0,
<0, ![]() ).
).
Nakreslíme obrázek
![]()
![]()
> plot(exp(1)^(-3*x),x = 0..infinity);
![[Maple Plot]](images/index497.gif)
Plochu obrazce omezeného křivkou y = f(x), osou x a přímkami x = a, y = b vypočteme podle známého vzorce
P = 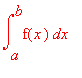
V našem případě je tedy plocha :
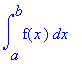
> P:=Int(exp(1)^(-3*x),x=0..infinity)=int(exp(1)^(-3*x),x=0..infinity);
>
10.3 Příklad 3.
Vypočtěte hodnotu
integrálu nevlastního vzhledem k nespojitosti v mezi 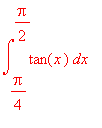
![]()
> IN:=Int(tan(x),x = Pi/4 .. Pi/2)=int(tan(x),x = Pi/4 .. Pi/2);
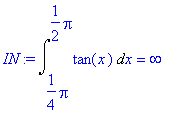
Protože hodnota tohoto integrálu je ![]() , víme, že není definován, tedy diverguje
, víme, že není definován, tedy diverguje
![]()
>
10.4 Příklad 4.
Vypočtěte 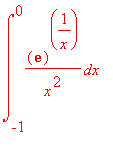
> Int(exp(1)^(1/x)/(x^2),x = -1 .. 0)=int(exp(1)^(1/x)/(x^2),x =-1 .. 0);
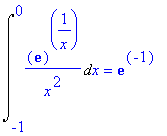
>
10.5 Příklad 5.
Vypočtěte objem tělesa vzniklého rotací křivky
y = 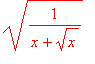 kolem osy x na intervalu <0,1>.
kolem osy x na intervalu <0,1>.
Vidíme, že integrál je nevlastní vzhledem k dolní mezi. Objem vypočítáme pomocí Maple takto:
> restart;
> V:=Pi*Int((sqrt(1/(x+sqrt(x))))^2, x=0..1)=Pi*int((sqrt(1/(x+sqrt(x))))^2, x=0..1);
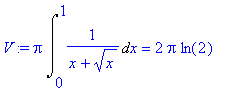
> plot(sqrt(1/(x+sqrt(x))),x=0..1);
![[Maple Plot]](images/index510.gif)
> plot(sqrt(1/(x+sqrt(x))),x=0..0.1);
![[Maple Plot]](images/index511.gif)