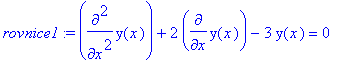
Ing. Jana Hřebíčková
Mgr. Jaroslav Ráček
Ing. Jana Slaběňáková
Fakulta stavební, Vysoké učení technické
Fakulta informatiky, Masarykova univerzita
Brno
2001
Obsah:
Diferenciální rovnice druhého a vyšších řádů v Maple 7 - řešené příklady - mws verze
1. Homogenní rovnice
1.1 Příklad 1
mws verzeNaleznete obecne reseni rovnice y" + 2 y' - 3 y = 0.
> restart;
> rovnice1:=diff(y(x),x$2)+2*diff(y(x),x)-3*y(x)=0;
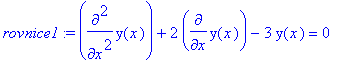
Jedna se o homogenni rovnici druheho radu. Jeji
reseni hledame ve tvaru y ( x )= 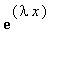
> tvar_reseni:=y(x)=exp(lambda*x);
![]()
Dosazenim do zadane rovnice dostaneme po upravach charakteristickou rovnici.
> subs(tvar_reseni,rovnice1);
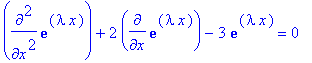
> simplify(%);
![]()
Protoze vyraz 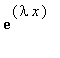 je vzdy
vetsi nez nula, muzeme jim rovnici vydelit.
je vzdy
vetsi nez nula, muzeme jim rovnici vydelit.
> char_rovnice:=simplify(%/exp(lambda*x));
![]()
Vypocteme koreny charakteristicke rovnice.
> solve(char_rovnice,lambda);
![]()
Charakteristicka rovnice ma tedy 2 realne ruzne koreny.
Fundamentalni system reseni ma tvar:
> reseni1:=subs(lambda=1,tvar_reseni); reseni2:=subs(lambda=-3,tvar_reseni);
![]()
![]()
Urcime wronskian nalezenych reseni pomoci stejnojmenneho prikazu, ktery je soucasti knihovny linalg ,
> with(linalg): wronskian([rhs(reseni1),rhs(reseni2)],x);
![matrix([[exp(x), exp(-3*x)], [exp(x), -3*exp(-3*x)]...](images/index11.gif)
a vypocteme ho.
> det(%);
![]()
Protoze wronskian je pro vsechna realna x nenulovy, jsou obe reseni linearne nezavisla.
Linearni kombinaci nalezenych reseni dostaneme obecne reseni.
> ob_reseni:=y(x)=c[1]*rhs(reseni1)+c[2]*rhs(reseni2);
![]()
Vysledek porovname s vystupem prikazu dsolve .
> dsolve(rovnice1,y(x));
![]()
Spravnost vypoctu overime dosazenim obecneho reseni do puvodni rovnice.
> subs(ob_reseni,rovnice1);
![diff(c[1]*exp(x)+c[2]*exp(-3*x),`$`(x,2))+2*diff(c[...](images/index15.gif)
> simplify(%);
![]()
Do jednoho obrazku zobrazime nekolik partikularnich
reseni pro ruzne hodnoty konstant ![]() ,
, ![]() .
.
> part1:=plot(subs(c[1]=1,c[2]=1,rhs(ob_reseni)),x=-.5..2,color=blue): part2:=plot(subs(c[1]=1,c[2]=-1,rhs(ob_reseni)),x=-.5..2,color=blue): part3:=plot(subs(c[1]=1,c[2]=-2,rhs(ob_reseni)),x=-.5..2,color=blue): part4:=plot(subs(c[1]=-1,c[2]=-1,rhs(ob_reseni)),x=-.5..2,color=red): part5:=plot(subs(c[1]=-1,c[2]=1,rhs(ob_reseni)),x=-.5..2,color=red): part6:=plot(subs(c[1]=-1,c[2]=2,rhs(ob_reseni)),x=-.5..2,color=red): with(plots): display([part1,part2,part3,part4,part5,part6],tickmarks=[4,3],thickness=1);
Dale zobrazime grafy partikularnich reseni prochazejicich bodem [0,0]. Do obecneho reseni tedy dosadime odpovidajici pocatecni podminku y (0) = 0
> dosazeni1:=0=subs(x=0,rhs(ob_reseni));
![]()
a vyjadrime jednu konstantu pomoci druhe.
> konst1:=solve(dosazeni1,{c[1]});
![]()
Do obecneho reseni dosadime vyjadreni konstanty ![]() .
.
> partVBode:=y(x)=subs(konst1,rhs(ob_reseni));
![]()
Urcime rovnici tecny ke krivce tohoto reseni v bode ![]() = 0 ve tvaru y = kx + q . Smernici k
zjistime pomoci derivace v bode
= 0 ve tvaru y = kx + q . Smernici k
zjistime pomoci derivace v bode ![]() , usek q
je funkcni hodnota v bode
, usek q
je funkcni hodnota v bode ![]() .
.
> tecna1:=y(x)=simplify(subs(x=0,diff(rhs(partVBode),x))*x+subs(x=0,rhs(partVBode)));
![]()
Nyni budeme animovat partikularni reseni
prochazejici bodem [0,0] spolecne s jeho tecnou v ![]() = 0 pro hodnotu
konstanty
= 0 pro hodnotu
konstanty ![]() menici se od -2 do 2. Vsimneme si, ze smernice tecny
je pro ruzna partikularni reseni ruzna.
menici se od -2 do 2. Vsimneme si, ze smernice tecny
je pro ruzna partikularni reseni ruzna.
> krivka1:=animate(rhs(partVBode),x=-1..3,c[2]=-2..2,color=blue,frames=80): krivka2:=animate(rhs(tecna1),x=-1..1.5,c[2]=-2..2,color=red,frames=80): display({krivka1,krivka2},thickness=2);
Nyní hledejme reseni ktera maji v bode ![]() tecnu se smernici 0 (tedy splnujici podminku y' (0) = 0).
tecnu se smernici 0 (tedy splnujici podminku y' (0) = 0).
dosazeni2:=0=subs(x=0,rhs(diff(ob_reseni,x)));
![]()
Vyjadrime jednu konstantu pomoci druhe.
> konst1:=solve(dosazeni2,{c[1]});
![]()
Do obecneho reseni dosadime vyjadreni konstanty ![]() .
.
> partSeSmer:=y(x)=subs(konst1,rhs(ob_reseni));
![]()
Opet urcime rovnici tecny v bode ![]() .
.
> tecna2:=y(x)=simplify(subs(x=0,diff(rhs(partSeSmer),x))*x+subs(x=0,rhs(partSeSmer)));
![]()
Nyni budeme animovat partikularni reseni majici v
bode ![]() = 0 derivaci 0, opet pro hodnoty
= 0 derivaci 0, opet pro hodnoty ![]() od -2 do 2. Vsimneme si, ze funkcni hodnota v bode
od -2 do 2. Vsimneme si, ze funkcni hodnota v bode ![]() je pro ruzna partikularni reseni ruzna.
je pro ruzna partikularni reseni ruzna.
> krivka3:=animate(rhs(partSeSmer),x=-1..3,c[2]=-2..2,frames=80,color=blue): krivka4:=animate(rhs(tecna2),x=-1..1.5,c[2]=-2..2,frames=80,color=red): display({krivka3,krivka4},thickness=2);
1.2 Příklad 2
mws verzeUrcete partikularni reseni rovnice y" + 4 y' + 5 y = 0 pro pocatecni podminky y (0) = -1 , y' (0) = 5 .
> restart;
> rovnice2:=diff(y(x),x$2)+4*diff(y(x),x)+5*y(x)=0;
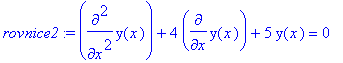
Jde o homogenni rovnici druheho radu. Charakteristickou rovnici urcime pouzitim procedury char ze souboru difproc.m
> read "difproc.m": char_rovnice:=char(rovnice2,y(x));
![]()
a nalezneme jeji koreny.
> solve(char_rovnice,lambda);
![]()
Charakteristicka rovnice ma tedy 2 komplexni sdruzene koreny.
Zname-li koreny charakteristicke rovnice muzeme vyjadrit obecne reseni.
> ob_reseni:=y(x)=c[1]*exp(-2*x)*cos(x)+c[2]*exp(-2*x)*sin(x);
![]()
Vypocteme derivaci obecneho reseni.
> derivace:=diff(ob_reseni,x);
![]()
Podminku y (0) = -1 dosadime do obecneho reseni a podminku y' (0) = 5 do derivace obecneho reseni.
> dosazeni1:=-1=subs(x=0,rhs(ob_reseni)); dosazeni2:=5=subs(x=0,rhs(derivace));
![]()
![]()
Ze ziskane soustavy rovnic vypocteme konstanty ![]() a
a ![]() .
.
> konstanty:=solve({dosazeni1,dosazeni2},{c[1],c[2]});
![]()
Dosazenim konstant do obecneho reseni dostaneme hledane partikularni reseni.
> part_reseni:=subs(konstanty,ob_reseni);
![]()
Overime spravnost vypoctu pomoci prikazu dsolve .
> part_reseni1:=dsolve({rovnice2,y(0)=-1,D(y)(0)=5},y(x));
![]()
Pomoci prikazu DEplot z knihovny DEtools zobrazime graf
partikularniho reseni spolu s tecnou v bode ![]() . Rovnici
tecny hledame ve smernicovem tvaru, smernice odpovida derivaci v nule, usek na ose y je
funkcni hodnota v nule.
. Rovnici
tecny hledame ve smernicovem tvaru, smernice odpovida derivaci v nule, usek na ose y je
funkcni hodnota v nule.
> tecna:=y(x)=simplify(subs(x=0,diff(rhs(part_reseni),x))*x+subs(x=0,rhs(part_reseni)));
![]()
> graf_tecny:=plot(rhs(tecna),x=-.25..0.25,thickness=2,color=red): with(DEtools): graf_reseni:=DEplot(rovnice2,y(x),x=-.25..2.5,[[y(0)=-1,D(y)(0)=5]],stepsize=.05,linecolor=black,thickness=2): with(plots): display([graf_tecny,graf_reseni],tickmarks=[4,3]);
1.3 Příklad 3
mws verzeUrcete reseni Cauchyovy pocatecni ulohy y'' + 2 y' + y = 0 , y (0) = 2 , y' (0) = -1 .
> restart;
> rovnice3:=diff(y(x),x$2)+2*diff(y(x),x)+y(x)=0;
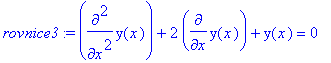
Pouzijeme proceduru char .
> read "difproc.m": char_rovnice:=char(rovnice3,y(x));
![]()
> solve(char_rovnice,lambda);
![]()
Charakteristicka rovnice ma dvojnasobny koren. K ziskani obecneho reseni pouzijeme proceduru hom , ktera hleda obecne reseni dane homogenni diferencialni rovnice.
> ob_reseni:=hom(rovnice3,y(x));
![]()
Do obecneho reseni a jeho derivace dosadime zadane pocatecni podminky.
> dosazeni1:=2=subs(x=0,rhs(ob_reseni)); dosazeni2:=-1=subs(x=0,rhs(diff(ob_reseni,x)));
![]()
![]()
Ze ziskane soustavy rovnic vypocteme konstanty ![]() a
a ![]() .
.
> konstanty:=solve({dosazeni1,dosazeni2},{c[1],c[2]});
![]()
Hledane partikularni reseni dostaneme dosazenim konstant do obecneho reseni.
> part_reseni:=y(x)=subs(konstanty,rhs(ob_reseni));
![]()
Overime, zda nalezene partikularni reseni vyhovuje zadane rovnici.
> simplify(subs(part_reseni,rovnice3));
![]()
Pro nalezeni partkularniho reseni muzeme pouzit take proceduru hom , ve ktere jako treti parametr zadame pocatecni podminky,
> podminky:=[[0,2],[0,-1]];
![]()
> part_reseni2:=hom(rovnice3,y(x),podminky);
![]()
nebo lze pouzit proceduru part , ktera hleda partikularni reseni primo z obecneho reseni.
> part_reseni3:=part(ob_reseni,podminky);
![]()
Zobrazime graf partikularniho reseni.
> plot(rhs(part_reseni),x=-2.5..4,thickness=2);
1.4 Příklad 4
mws verzeUrcete partikularni reseni rovnice y''''' - y' = 0 pro pocatecni podminky y (0) = 0 , y' (0) = 1 , y" (0) = 0 , y'" (0) = 1 , y'''' (0) = 2 .
> restart;
> rovnice4:=diff(y(x),x$5)-diff(y(x),x)=0;
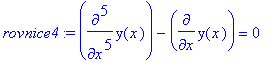
> podminky:=[[0,0],[0,1],[0,0],[0,1],[0,2]];
![]()
Jde o homogenni rovnici 5. radu. Urcime koreny charakteristicke rovnice a nalezneme obecne reseni.
> read "difproc.m": solve(char(rovnice4,y(x)),lambda);
![]()
> ob_reseni:=hom(rovnice4,y(x));
![]()
Pomoci procedury part urcime hledane partikularni reseni
> part_reseni:=part(ob_reseni,podminky);
![]()
a zkontrolujeme, zda je resenim zadane rovnice.
> simplify(subs(part_reseni,rovnice4));
![]()
Zobrazime graf nalezeneho partikularniho reseni.
> plot(rhs(part_reseni),x=-11..2.2,thickness=2,scaling=constrained);
2. Nehomogenní rovnice – Metoda variace konstant
2.1 Příklad 5
mws verzeNaleznete obecne reseni rovnice y'' - 2y' + y = ![]() / x .
/ x .
> restart;
> rovnice1:=diff(y(x),x$2)-2*diff(y(x),x)+y(x)=exp(x)/x;
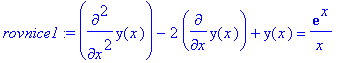
Jde o nehomogenni diferencialni rovnici 2. radu, kterou budeme resit metodou variace konstant.
Prislusna homogenni rovnice ma tvar
> hom_rovnice:=lhs(rovnice1)=0;
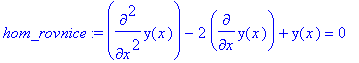
Uzitim procedury char spocitame koreny charakteristicke rovnice a pomoci procedury hom nalezneme obecne reseni homogenni rovnice.
> read "difproc.m": solve(char(hom_rovnice,y(x)),lambda);
![]()
> ob_res_hom:=hom(hom_rovnice,y(x));
![]()
Partikularni reseni nehomogenni rovnice budeme hledat ve tvaru
> tvar:=subs(c[1]=K[1](x),c[2]=K[2](x),ob_res_hom);
![]()
ktery jsme dostali nahrazenim konstant ![]() ,
, ![]() funkcemi
funkcemi ![]() ,
, ![]() .
.
Vypocteme prvni derivaci.
> der1:=diff(tvar,x);
![]()
Klademe:
> podminka1:=op(1,rhs(der1))+op(3,rhs(der1))=0;
![]()
Dosazenim dostavame:
> der1upr:=lhs(der1)=rhs(der1)-lhs(podminka1);
![]()
> der2:=diff(der1upr,x);
,x)*exp(x...](images/index86.gif)
Dosazenim do puvodni rovnice mame:
> podminka2:=simplify(subs(diff(y(x),x$2)=rhs(der2),y(x)=rhs(tvar),rovnice1));
,x)*exp(x)+diff(K[2](x),x...](images/index87.gif)
V ziskane soustave rovnic zavedeme pro jednoduchost
substituci - prvni derivace hledanych funkci ![]() ,
, ![]() oznacime A, B .
oznacime A, B .
> soustava:=subs({diff(K[1](x),x)=A,diff(K[2](x),x)=B},{podminka1,podminka2});
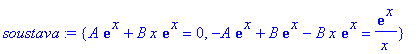
Vypocteme prvni derivace funkci ![]() ,
, ![]() a ulozime je do promennych A, B
.
a ulozime je do promennych A, B
.
> konst_der:=solve(soustava,{A,B}); assign(konst_der);
![]()
Integraci A a B dostaneme vzhledem ke stanovene substituci funkce ![]() ,
, ![]() .
.
> konst1:=int(A,x);
![]()
> konst2:=int(B,x);
![]()
Hledane partikularni reseni pak ma tvar
> part_reseni:=simplify(subs(K[1](x)=konst1,K[2](x)=konst2,tvar));
![]()
Obecne reseni nehomogenni rovnice je souctem obecneho reseni prislusne homogenni rovnice a partikularniho reseni nehomogenni rovnice.
Jelikoz Maple pri integraci, jejimz vysledkem je funkce obsahujici prirozeny logaritmus, nezohlednuje definicni obor (tj. neuzavira argument prirozeneho logaritmu do absolutni hodnoty), vyresime tuto odlisnost rucnim prepsanim.
> ob_reseni:=y(x)=rhs(ob_res_hom)-x*exp(x)+ln(abs(x))*x*exp(x);
![]()
Reseni ziskane prikazem dsolve bude mit take tuto odlisnost.
> ob_dsolve:=dsolve(rovnice1,y(x));
![]()
Nyni zobrazime grafy vybranych partikularnich reseni
pro pevnou hodnotu konstanty ![]() , za konstantu
, za konstantu ![]() postupne volime hodnoty 1, 0, a -1.
postupne volime hodnoty 1, 0, a -1.
> with(plots): g1:=plot(subs(c[1]=1,c[2]=1,rhs(ob_reseni)),x=-2.5..1.1,color=red): g2:=plot(subs(c[1]=1,c[2]=0,rhs(ob_reseni)),x=-2.5..1.1,color=blue): g3:=plot(subs(c[1]=1,c[2]=-1,rhs(ob_reseni)),x=-2.5..1.1,color=black): display(g1,g2,g3,thickness=2,tickmarks=[4,3]);
Chceme-li vykreslit graf partikularniho reseni pro stejny interval promenne x jako v predchozim obrazku pomoci prikazu DEplot , skonci vypocet chybou.
> with(DEtools): g4:=DEplot(rovnice1,y(x),x=-2.5..1.1,[[y(1)=1,D(y)(1)=-1]],stepsize=.05):
Error, (in DEtools/DEplot/drawlines) Stopping integration due to division by zero
2.2 Příklad 6
mws verzeNaleznete obecne reseni rovnice y'' + 4y = 1/ sin(2x)
> restart;
> rovnice2:=diff(y(x),x$2)+4*y(x)=1/sin(2*x);
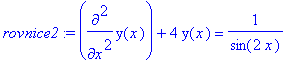
Vypocteme koreny charakteristicke rovnice.
> read "difproc.m": solve(char(lhs(rovnice2)=0,y(x)),lambda);
![]()
Nalezneme obecne reseni prislusne homogenni rovnice pomoci procedury hom . Pomoci volitelneho parametru "fund" nechame zobrazit take fundamentalni system zadane rovnice, ktery budeme potrebovat pri dalsim vypoctu.
> ob_res_hom:=hom(lhs(rovnice2)=0,y(x),"fund");
![]()
![]()
Partikularni reseni nehomogenni rovnice budeme hledat v nasledujicim tvaru.
> tvar:=y(x)=subs(c[1]=K[1](x),c[2]=K[2](x),rhs(ob_res_hom));
![]()
Tak, jak je v praktickem vypoctu obvykle, vynechame
odvozeni a prejdeme rovnou k soustave rovnic pro prvni derivace neznamych funkci ![]() ,
, ![]() .
.
> podminka1:=diff(K[1](x),x)*fund[1]+diff(K[2](x),x)*fund[2]=0;
![]()
> podminka2:=diff(K[1](x),x)*diff(fund[1],x)+diff(K[2](x),x)*diff(fund[2],x)=rhs(rovnice2);
![]()
Vyresime danou soustavu, ve ktere pro jednoduchost
oznacime prvni derivace hledanych funkci ![]() ,
, ![]() symboly A, B .
symboly A, B .
> konst_der:=solve(subs(diff(K[1](x),x)=A,diff(K[2](x),x)=B,{podminka1,podminka2}),{A,B}); assign(konst_der);
![]()
Intregraci dostaneme hledane funkce ![]() ,
, ![]() .
.
> konst1:=int(A,x);
![]()
> konst2:=int(B,x);
![]()
Upravime vyjadreni prvni konstanty uzavrenim argumentu logaritmu do absolutni hodnoty.
> konst1upr:=1/4*ln(abs(sin(2*x)));
![]()
Vyjadrime obecne reseni nehomogenni rovnice.
> ob_reseni:=y(x)=rhs(ob_res_hom)+subs(K[1](x)=konst1upr,K[2](x)=konst2,rhs(tvar));
![]()
Vysledek muzeme overit pouzitim procedury varconst , ktera automatizuje predchozi postup pomoci Mapleovskeho programovaciho jazyka.Rozdil je pouze v pridane absolutni hodnote.
> varconst(rovnice2,y(x));
![]()
Vykreslime nektera partikularni reseni pro pevnou
hodnotu konstanty ![]() .
.
> with(plots): g1:=plot(subs(c[1]=0,c[2]=-1,rhs(ob_reseni)),x=-2.5..2.5,numpoints=200,color=red): g2:=plot(subs(c[1]=0,c[2]=0,rhs(ob_reseni)),x=-2.5..2.5,numpoints=200,color=blue): g3:=plot(subs(c[1]=0,c[2]=1,rhs(ob_reseni)),x=-2.5..2.5,numpoints=200,color=black): display(g1,g2,g3,thickness=2);
2.3 Příklad 7
mws verzeNaleznete partikularni reseni rovnice y''' + 2y'' + 4y' + 8y = 32cos2x pro pocatecni podminky y(0)=2, y'(0)=6, y''(0)=0 .
> restart;
> rovnice3:=diff(y(x),x$3)+2*diff(y(x),x$2)+4*diff(y(x),x)+8*y(x)=32*cos(2*x);
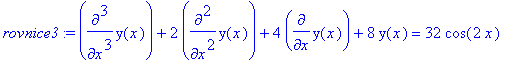
> podminky:=[[0,2],[0,6],[0,0]];
![]()
Pro informaci vypocteme koreny charakteristicke rovnice a vyjadrime obecne reseni prislusne homogenni rovnice.
> read "difproc.m": solve(char(lhs(rovnice3)=0,y(x)),lambda);
![]()
> hom(lhs(rovnice3)=0,y(x));
![]()
Pro nalezeni obecneho reseni nehomogenni rovnice pouzijeme proceduru varconst .
> ob_reseni:=varconst(rovnice3,y(x));
![]()
Do obecneho reseni a jeho prvni a druhe derivace postupne dosadime zadane pocatecni podminky.
> dosazeni1:=2=subs(x=0,rhs(ob_reseni));
![]()
> dosazeni2:=6=subs(x=0,diff(rhs(ob_reseni),x));
![]()
> dosazeni3:=0=subs(x=0,diff(rhs(ob_reseni),x$2));
![]()
Resenim soustavy dostaneme hodnoty neznamych
konstant ![]() ,
, ![]() ,
, ![]() .
.
> konstanty:=solve({dosazeni1,dosazeni2,dosazeni3},{c[1],c[2],c[3]});
![]()
Dosazenim do obecneho reseni dostaneme partikularni reseni vyhovujici zadanym pocatecnim podminkam.
> part_reseni:=y[p](x)=subs(konstanty,rhs(ob_reseni));
![]()
Partikularni reseni muzeme hledat take pomoci procedury part , nebo primo pouzitim procedury varconst .
> part(ob_reseni,podminky);
![]()
> varconst(rovnice3,y(x),podminky);
![]()
Dosazenim overime, zda toto reseni vyhovuje zadane rovnici.
> subs(y(x)=rhs(part_reseni),rovnice3): simplify(%);
![]()
Zobrazime graf nalezeneho partikularniho reseni.
> plot(rhs(part_reseni),x=-8..8,thickness=2,color=black);
3. Nehomogenní rovnice – Metoda neurčitých koeficientů
3.1 Příklad 8
mws verzeNaleznete obecne reseni nehomogenni rovnice y'' -
9y = 9 ![]() .
.
> restart;
> rovnice1:=diff(y(x),x$2)-9*y(x)=9*x^2;
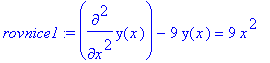
Vypocteme koreny charakteristicke rovnice a nalezneme obecne reseni prislusne homogenni rovnice.
> read "difproc.m":
> solve(char(lhs(rovnice1)=0,y(x)),lambda);
![]()
> ob_res_hom:=hom(lhs(rovnice1)=0,y(x));
![]()
Prava strana zadane rovnice je typu 1. Cislo 0 neni korenem charakteristicke rovnice, takze partikularni reseni budeme hledat ve tvaru polynomu druheho stupne.
> part_reseni:=x^0*(A*x^2+B*x+C);
![]()
Tvar hledaneho partikularniho reseni dosadime do zadane nehomogenni rovnice a zjednodusime ji.
> dosazeni:=simplify(subs(y(x)=part_reseni,rovnice1));
![]()
Vysledna rovnice obsahuje tri nezname koeficienty. Postupnym dosazenim hodnot 1,2,3 za promennou x dostaneme tri rovnice pro koeficienty A,B,C . Ziskanou soustavu rovnic vyresime.
> koef:=solve({seq(subs(x=i,dosazeni),i=1..3)},{A,B,C});
![]()
Dosazenim vypoctenych koeficientu do tvaru partikularniho reseni dostaneme jedno konkretni partikularni reseni.
> part_reseni:=subs(koef,part_reseni);
![]()
Obecne reseni nehomogenni rovnice je souctem obecneho reseni prislusne homogenni rovnice a libovolneho partikularniho reseni nehomogenni rovnice.
> ob_reseni:=y(x)=rhs(ob_res_hom)+part_reseni;
![]()
Dosazenim overime, ze nalezene reseni vyhovuje zadane rovnici.
> overeni:=simplify(subs(ob_reseni,rovnice1));
![]()
Zobrazime grafy nekolika partikularnich reseni.
> with(plots): grafy1:=seq(plot(subs(c[1]=i,c[2]=1,rhs(ob_reseni)),x=-0.45 .. 0.45),i=-1..1): grafy2:=seq(plot(subs(c[1]=1,c[2]=i,rhs(ob_reseni)),x=-0.45 .. 0.45),i=-1..0): display(grafy1,grafy2);
3.2 Příklad 9
mws verzeNaleznete obecne reseni nehomogenni rovnice y'' + 9y = x sin( 3x ).
> restart;
> rovnice2:=diff(y(x),x$2)+9*y(x)=x*sin(3*x);
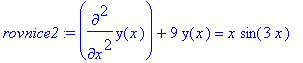
Vypocteme koreny charakteristicke rovnice a urcime obecne reseni prislusne homogenni rovnice
> read "difproc.m": solve(char(lhs(rovnice2)=0,y(x)),lambda);
![]()
> ob_res_hom:=hom(lhs(rovnice2)=0,y(x));
![]()
Prava strana zadane rovnice je typu 3, pricemz
polynom P ( x
) = 0, ![]() = 0,
= 0, ![]() = 3, cislo 0 + 3 i je jednoduchym
korenem charakteristicke rovnice. Polynom x je stupne 1, tedy partikularni reseni
budeme hledat ve tvaru
= 3, cislo 0 + 3 i je jednoduchym
korenem charakteristicke rovnice. Polynom x je stupne 1, tedy partikularni reseni
budeme hledat ve tvaru
> part_reseni:=x^1*((A*x+B)*cos(3*x)+(C*x+D)*sin(3*x));
![]()
Tvar hledaneho partikularniho reseni dosadime do zadane nehomogenni rovnice.
> dosazeni:=simplify(subs(y(x)=part_reseni,rovnice2));
![]()
Pro zjisteni hodnot neznamych koeficientu A , B , C , D budeme potrebovat ctyri rovnice, ktere ziskame postupnym dosazenim cisel 1, 2, 3, 4 za promennou x .
> koef:=solve({seq(subs(x=i,dosazeni),i=1..4)},{A,B,C,D});
![]()
Dosazenim vypoctenych koeficientu ziskame partikularni reseni.
> part_reseni:=subs(koef,part_reseni);
![]()
Jeho prictenim k obecnemu reseni homogenni rovnice dostaneme obecne reseni nehomogenni rovnice.
> ob_reseni:=y(x)=rhs(ob_res_hom)+simplify(part_reseni);
![]()
Vysledek porovname s vystupem procedury neurkoef , ktera je soucasti souboru difproc.m . Tato procedura hleda obecne reseni nehomogenni rovnice, kterou je mozne resit metodou neurcitych koeficientu (automatizuje predchozi postup pomoci Mapleovskeho programovaciho jazyka).
> neurkoef(rovnice2,y(x));
![]()
Zobrazime grafy nekterych partikularnich reseni pro
pevnou hodnotu konstanty ![]() = 0.
= 0.
> with(plots): graf1:=plot(subs(c[1]=0,c[2]=-1,rhs(ob_reseni)),x=-4..4,color=black): graf2:=plot(subs(c[1]=0,c[2]=0,rhs(ob_reseni)),x=-4..4,color=blue): graf3:=plot(subs(c[1]=0,c[2]=1,rhs(ob_reseni)),x=-4..4,color=red): display(graf1,graf2,graf3,thickness=2);
Warning, the name changecoords has been redefined
Pro pevnou hodnotu konstanty ![]() budeme partikularni reseni animovat pro vetsi interval promenne x.
budeme partikularni reseni animovat pro vetsi interval promenne x.
> animate(subs(c[1]=0,rhs(ob_reseni)),x=-8..8,c[2]=-2..6,numpoints=150,frames=100,thickness=2,tickmarks=[4,3]);
3.3 Příklad 10
mws verzeNaleznete partikularni reseni rovnice y'' + 9
y = sin( x ) - 2 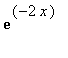 splnujici pocatecni podminky y
(0) = 3/5, y' (0) = 3/10.
splnujici pocatecni podminky y
(0) = 3/5, y' (0) = 3/10.
> restart;
> rovnice3:=diff(y(x),x$2)+y(x)=sin(x)-2*exp(-2*x);
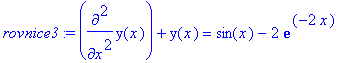
Vypocteme koreny charakteristicke rovnice.
> read "difproc.m": solve(char(lhs(rovnice3)=0,y(x)),lambda);
![]()
Prava strana rovnice je typu 4, presneji je souctem pravych stran typu 3 a 2. Pouzijeme tzv. princip superpozice. Vytvorime dve nove rovnice se stejnymi levymi stranami, pravou stranu "rozdelime" tak, aby kazda jeji cast byla typu 1, 2 nebo 3. Dale budeme resit obe ziskane rovnice paralelne.
> rce1:=lhs(rovnice3)=op(1,rhs(rovnice3)); rce2:=lhs(rovnice3)=op(2,rhs(rovnice3));
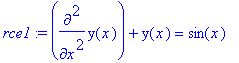
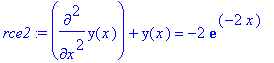
Vyjadrime tvary partikularnich reseni. U prvni
rovnice je ![]() = 1 a cislo i je
pritom jednoduchym korenem charakteristicke rovnice. Proto zde nesmime zapomenout na clen
= 1 a cislo i je
pritom jednoduchym korenem charakteristicke rovnice. Proto zde nesmime zapomenout na clen ![]() .
.
> part_reseni1:=x^1*(A*cos(x)+B*sin(x)); part_reseni2:=C*exp(-2*x);
![]()
![]()
Tvary partikularnich reseni dosadime do prislusnych rovnic a vypocteme nezname koeficienty.
> dosazeni1:=simplify(subs(y(x)=part_reseni1,rce1)); dosazeni2:=simplify(subs(y(x)=part_reseni2,rce2));
![]()
![]()
> koef1:=solve({seq(subs(x=i,dosazeni1),i=1..2)},{A,B}); koef2:=solve(dosazeni2,{C});
![]()
![]()
Dosazenim koeficientu dostaneme hledana partikularni reseni.
> part_reseni1:=subs(koef1,part_reseni1); part_reseni2:=subs(koef2,part_reseni2);
![]()
![]()
Partikularni reseni zadane rovnice lze nyni vyjadrit jako soucet obou nalezenych partikularnich reseni. Pak obecne reseni ma nasledujici tvar.
> ob_reseni:=y(x)=rhs(hom(lhs(rovnice3)=0,y(x)))+ (part_reseni1+part_reseni2);
![]()
Pro nalezeni konkretniho partikularniho reseni, ktere se pozaduje v zadani, musime dane pocatecni podminky dosadit do obecneho reseni a jeho derivace.
> podminka1:=3/5=subs(x=0,rhs(ob_reseni));
![]()
> podminka2:=3/10=subs(x=0,diff(rhs(ob_reseni),x));
![]()
Ze ziskane soustavy rovnic vypocteme konstanty ![]() a
a ![]() . Ty potom dosadime do obecneho reseni.
. Ty potom dosadime do obecneho reseni.
> konst:=solve({podminka1,podminka2},{c[1],c[2]});
![]()
> part_reseni:=subs(konst,ob_reseni);
![]()
Pro nalezeni partikularniho reseni muzeme pouzit take proceduru neurkoef nebo proceduru part .
> podminky:=[[0,3/5],[0,3/10]];
![]()
> neurkoef(rovnice3,y(x),podminky);
![]()
> part(ob_reseni,podminky);
![]()
Overime, zda nalezene reseni vyhovuje zadane rovnici a zobrazime ho.
> simplify(subs(part_reseni,rovnice3));
![]()
> plot(rhs(part_reseni),x=-1.3..17.5,thickness=2);
3.4 Příklad 11
mws verzeNaleznete partikularni reseni rovnice y'''''
- 2 y'''' - 2 y''' + 4 y'' + y' - 2 y =  splnujici pocatecni podminky y (0) =
1, y' (0) = -3, y'' (0) = 5/2, y''' (0) = -4, y''''
(0) = -7/2.
splnujici pocatecni podminky y (0) =
1, y' (0) = -3, y'' (0) = 5/2, y''' (0) = -4, y''''
(0) = -7/2.
> restart;
> rovnice4:=diff(y(x),x$5)-2*diff(y(x),x$4)-2*diff(y(x),x$3)+4*diff(y(x),x$2)+diff(y(x),x)-2*y(x)=25*exp(-x)*cos(x);
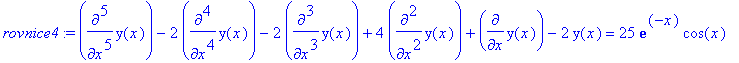
> podminky:=[[0,1],[0,-3],[0,5/2],[0,-4],[0,-7/2]];
![]()
Jde o rovnici 5. radu, kterou lze resit metodou neurcitych koeficientu. Koreny charakteristicke rovnice lze ziskat vytykanim a pouzitim znamych vzorcu.
> read "difproc.m": solve(char(lhs(rovnice4)=0,y(x)));
![]()
Pomoci procedury neurkoef dostaneme obecne reseni zadane rovnice.
> ob_reseni:=neurkoef(rovnice4,y(x));
![]()
Pomoci procedury part urcime hledane partikularni reseni.
> part_reseni:=part(ob_reseni,podminky);
![]()
Overime, zda nalezene reseni vyhovuje dane rovnici a zobrazime jej pro vhodny rozsah promenne x .
> simplify(subs(part_reseni,rovnice4));
![]()
> plot(rhs(part_reseni),x=-3.4..2.3,thickness=2);
>
4. Ukázky aplikací rovnic 2. řádu
4.1 Příklad 12 - lineární oscilátor
4.4 Příklad 15 - tlumící funkce
5. Procedury
5.1 difproc.mws
> mujsort:=proc(a) local j,k,b,c,newa; newa:=a; b:=[]; for j to nops(newa) do b:=[op(b),convert(newa[j],string)]; od; newa:=b; b:=sort(b,lexorder); c:=[]; for j to nops(b) do for k while not(b[j]=newa[k]) do od; c:=[op(c),a[k]]; od; c; end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> PrectiProm:=proc(prom::anything) local st,i; global nez,zav; st:=convert(prom,string); for i from 1 while not(substring(st,i)="(") do od; nez:=convert(substring(st,i+1..length(st)-1),symbol); zav:=convert(substring(st,1..i-1),symbol); end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> char:=proc(DR::equation,promen::anything) PrectiProm(promen); simplify(simplify(subs(zav(nez)=exp(lambda*nez),DR))/exp(lambda*nez)): end;
![]()
> part:=proc(OR,podm) local i,soust,konst; PrectiProm(lhs(OR)); soust:={op(2,op(1,podm))=simplify(subs(nez=op(1,op(1,podm)),rhs(OR)))}; for i from 2 to nops(podm) do soust:=soust union {op(2,op(i,podm))=simplify(subs(nez=op(1,op(i,podm)),diff(rhs(OR),nez$(i-1))))} od; konst:=seq(c[i],i=1..nops(podm)); y(x)=subs(solve(soust,{konst}),rhs(OR)); end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> sol:=proc(r::anything,n::integer) local res; if type(r,complexcons) then if type(r,realcons) then res:=nez^(n-1)*exp(r*nez) else if abs(Im(r))=Im(r) then res:=nez^(n-1)*exp(Re(r)*nez)*cos(abs(Im(r))*nez) else res:=nez^(n-1)*exp(Re(r)*nez)*sin(abs(Im(r))*nez); fi; fi else error "sorry, tohle neumim."; fi end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> hom:=proc() global fund; local E,promenne,koreny,nas,i,prava,s; E:=args[1]; promenne:=args[2];koreny:=mujsort([solve(char(E,promenne),lambda)]); nas:=1; fund:=[sol(koreny[1],nas)]; for i from 2 to nops(koreny) do if koreny[i]=koreny[i-1] then nas:=nas+1 else nas:=1; fi; fund:=[op(fund),sol(koreny[i],nas)]; od; prava:=0; for s to nops(fund) do prava:=prava+c[s]*fund[s] od; if nargs=3 then if args[3]="fund" then print(fund); zav(nez)=prava else part(zav(nez)=prava,args[3]) fi; else zav(nez)=prava fi; end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> varconst:=proc() local j,p,n,konst,soust,konstder,prava,DR,prome; DR:=args[1]; prome:=args[2]; hom(lhs(DR)=0,prome); n:=nops(fund); soust:={sum(k[i]*fund[i],i=1..n)=0}; for j from 1 to n-2 do soust:=soust union {sum(k[i]*diff(fund[i],nez$j),i=1..n)=0}; od; soust:=soust union {sum(k[i]*diff(fund[i],nez$n-1),i=1..n)=rhs(DR)}; konstder:=mujsort(simplify(solve(soust,{seq(k[h],h=1..n)}))); konst:=map(a -> simplify(int(rhs(a),nez)),konstder); prava:=sum(c[i]*fund[i],i=1..n)+simplify(sum(fund[i]*konst[i],i=1..n)); if nargs=3 then part(zav(nez)=prava,args[3]) else zav(nez)=prava; fi; end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> param:=proc(pr) local sez, V
,prvek, i; if type(pr,`function`) or type(pr,`polynom`) then
if (op(0,pr) = `sin`) or (op(0,pr) = `cos`) then
[0, coeff(op(pr),x), 0];
elif op(0,pr) = `exp` then
[coeff(op(pr),x), 0, 0]
elif type(pr,`polynom`) then
[0, 0, degree(pr,x)]; fi;
else
sez:=[op(pr)];
V:=[0,0,0];
for i from 1 to nops(sez) do
prvek:=op(i,sez);
if (op(0,prvek) = `sin`) or (op(0,prvek) = `cos`) then
V:=subsop( 2 = coeff(op(prvek),x), V);
elif op(0,prvek) = `exp` then
V:=subsop( 1 = coeff(op(prvek),x), V);
elif type(prvek,`polynom`) then
V:=subsop( 3 = degree(prvek,x), V);
fi;
od;
V;
fi:
end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> neurkoef:=proc() local E,prom,i,j,par,kor,sez,L,P,alfa,beta,stupen,moc,R,S,Yg,Yp,ABrce; E:=args[1]; prom:=args[2]; L:=lhs(E); P:=rhs(E); kor:=roots(expand(lhs(char(L=0,prom))),lambda,I); Yg:=rhs(hom(L=0,prom)); if type(P,`+`) then sez:=[op(P)] else sez:=[P]; fi; for i to nops(sez) do par:=param(op(i,sez)); alfa:=par[1]; beta:=par[2]; stupen:=par[3]; moc:=0; for j from 1 to nops(kor) do if kor[j][1]=alfa+beta*I then moc:=kor[j][2]; fi; od; R:=0; S:=0; for j from 0 to stupen do R:=R+A[j]*nez^j; S:=S+B[j]*nez^j; od; Yp:=nez^moc*exp(alfa*nez)* (R*cos(beta*nez)+S*sin(beta*nez)); ABrce:=normal(simplify(subs(zav(nez)=Yp,L)))=sez[i]; Yp:=simplify(subs(solve({seq(subs(nez=j,ABrce),j=1..2*stupen+2)}),Yp)); Yg:=simplify(Yg+Yp); od; if nargs=3 then part(zav(nez)=Yg,args[3]) else zav(nez)=Yg; fi; end;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> save PrectiProm,char,part,sol,hom,varconst,mujsort,param,neurkoef,"difproc.m":
>