Ing. Jana Hřebíčková
Mgr. Jaroslav Ráček
Ing. Jana Slaběňáková
Fakulta stavební, Vysoké učení technické
Fakulta informatiky, Masarykova univerzita
Brno
2001
Obsah:
Diferenciální počet v Maple 7 - mws verze
1. Definice funkce - ukázky
> restart;
Matematickou funkci můžeme v systému Maple 7 definovat dvěma základními způsoby.
pomocí příkazu unapply
Oba dva způsoby definice matematické funkce ukazují následující příkazy systému Maple:> f:=x^5;
![]()
> g:=x->x^3;
![]()
> f:=unapply(f,x);
![]()
> g:=g(x);
![]()
> f(3);
![]()
> subs(x=3,g);
![]()
Pro skládání funkcí se v Maple používá operátor @. Jeho použití opět ukazují následující příkazy.
> h:=x->exp(sin(x^3));
![]()
> f:=x->x^5;
![]()
> (f@h)(x);
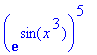
> (h@f)(x);
![]()
>
Základním příkazem pro vykreslení grafu funkce je příkaz plot:
> plot (f(x),x=-3..3, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index11.gif)
> with(plots):
Warning, the name changecoords has been redefined
> p1:=plot (f(x),x=-3..3,axesfont=[TIMES,ROMAN,15], labelfont=[TIMES,ROMAN,15]):
> p2:=plot (g,x=-3..3, axesfont=[TIMES,ROMAN,15],
> labelfont=[TIMES,ROMAN,15]):
> display({p1,p2});
![[Maple Plot]](images/index12.gif)
> plot ({f(x),g},x=-3..3, axesfont=[TIMES,ROMAN,15],
> labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index13.gif)
>
2. Limita
2.1 Vysvětlení limity na příkladech
2.1.1 Vlastní limita ve vlastním bodě
Příklad:
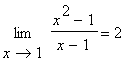
Nejdříve funkci nakreslíme
> restart;
> with(plots):
Warning, the name changecoords has been redefined
> p1:=plot ((x^2-1)/(x-1), x=-2..4, y=-1..5, labelfont=[TIMES,ROMAN,15]):
> p2:=plot({[1, t, t=0..2],[t,2, t=0..1]}, linestyle=2,symbol=point,color=blue):
> p3:=plot({[1,2]}, style=point, symbol=circle):
> display({p1,p2,p3},axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index15.gif)
>
2.1.2 Nevlastní limita ve vlastním bodě
Příklad:
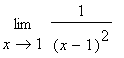 =
= ![]()
Zadanou funkci nakreslíme
> with(plots):
> p1:=plot (1/(x-1)^2, x=-1..3, y=0..20, discont=true,
> labelfont=[TIMES,ROMAN,15]):
> p2:=plot({[1,0]}, style=point, symbol=circle):
> p3:=plot([1,t,t=0..infinity], linestyle=3):
> display({p1, p2, p3}, axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index18.gif)
>
2.1.3 Vlastní limita v nevlastním bodě
Příklad:
![]() =
= ![]()
Zadanou funkci nakreslíme
> with(plots):
> p1:=plot (arctan(x), x=-10...10,labelfont=[TIMES,ROMAN,15]):
> p2:=plot({[t, Pi/2, t=0..10],[-1*s,-Pi/2, s=0..10]}, linestyle=3):
> p3:=plot({[0,Pi/2],[0,-Pi/2]}, style=point, symbol=circle):
> display({p1,p2,p3},axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index21.gif)
>
2.1.4 Nevlastní limita v nevlastním bodě
Příklad:
![]() =
= ![]()
> plot (ln(x), x=0..20, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index24.gif)
Příklad:
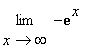 =
= ![]()
Zadanou funkci nakreslíme
> plot (-1*exp(x),x=-1..3, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index27.gif)
Příklad:
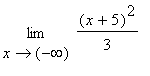 =
= ![]()
Graf funkce nakreslíme
> plot ((x+5)^2/3, x=-20..5, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index30.gif)
Příklad:
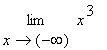 =
= ![]()
Zadanou funkci nakreslíme
> plot (x^3, x=-5..5, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index33.gif)
>
2.1.5 Ilustrace pravostranné a levostranné limity
Příklad:
signum(x) = ![PIECEWISE([-1, x < 0],[1, 0 < x])](images/index34.gif)
Tuto funkci nakreslíme pomocí Maple
> plot (signum(x), x=-3..3,y=-2..2, discont=true, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
Funkce není definována pro x = 0. Hodnoty jednostrnných limit určíme příkazy
![[Maple Plot]](images/index35.gif)
> limit(signum(x),x=0,left);
![]()
> limit(signum(x),x=0,right);
![]()
Hodnoty jednostranných limit jsou různé , ![]() tedy neexistuje.
tedy neexistuje.
Výpočet pomocí Maple:
> limit(signum(x),x=0);
![]()
>
2.2 Příkazy systému Maple pro výpočet limity
Pro výpočet limity slouží v systému Maple příkaz limit(expr,x=a,dir);
Parametry příkazu:
expr je algebraický výraz v proměnné x.
a je bod ,ve kterém se má limita počítat. Může to být libovolné reálné číslo, pro limity
v nevlastních bodech jsou určeny hodnoty -infinity a infinity
dir je nepovinný parametr. Může mít hodnotu left pro limitu zleva , resp. right pro limitu
zprava. Pokud parametr vynecháme, počítá se oboustranná limita.
Dále můžeme použít příkaz Limit , který limitu nevyhodnocuje. Hodnotu limity v tomto
případě určíme příkazem value. Vedle standardního příkazu můžeme použít i příkaz
Limit z knihovny student , který umožňujr i symbolické úpravy výrazů s limitami
(příkazem expand, případně combine ).
Knihovnu načteme příkazem with(student)
2.2.1 Příklad 1.
mws verzeUrčete limitu funkce f : y = 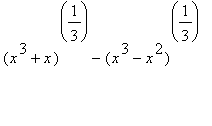 pro x->
pro x-> ![]()
> restart;
Nejdříve definujeme funkci
> f:=x->(x^3+x)^(1/3)-(x^3-x^2)^(1/3);
![]()
Nyní limitu vypočteme
> limit(f(x),x=infinity);
![]()
Výpočet i se zápisem:
> with(student,Limit):
> Limit(f(x),x=infinity):
> %=value(%);
![]()
>
Při symbolickém počítání limit často potřebujeme vytknout určitý výraz. K tomu slouží procedura vytkni(expr1,expr2), jejíž parametry jsou
expr1 je výraz, ze kterého budeme vytýkat
expr2 je výraz, který chceme vytknout
> restart;
> vytkni:=proc(f,expr)
> local cit,jm;
> cit:=numer(f);
> jm:=denom(f);
> cit:=expand(cit/expr);
> jm:=expand(jm/expr);
> cit/jm;
> end proc;
![]()
2.2.2 Příklad 2.
mws verzeUrčeme 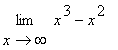
Můžeme použít příkaz limit , pokud však chceme demonstrovat postup, který používá při výpočtu student, použijeme příkaz vytkni .
> vytkni(x^3-x^2,x^3);
![]()
> with(student,Limit):
> expand(Limit(%%,x=infinity));
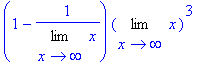
Víme, že ![]() =
=
![]() a 1/
a 1/ ![]() = 0 , hodnota limity je
tedy
= 0 , hodnota limity je
tedy
> value(%);
![]()
>
K testování spojitosti je určen příkaz iscont(expr,x=a..b,'closed') a discont(expr,x)
Parametry :
expr je algebraický výraz v x
a..b je interval
'closed' je volitelný parametr. Maple standartně určuje spojitost na otevřeném intervalu,
pokud uvedeme tento parametr, testuje Maple na uzavřeném intervalu.
Použití příkazů ukážeme v následujícím příkladu:
2.2.3 Příklad 3.
mws verzeVypočítejte limitu funkce f: y = 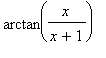 v bodech nespojitosti.
v bodech nespojitosti.
Definujeme funkci f :
> f:=x->arctan(x/(x+1));
![]()
Pomocí příkazu iscont zjistíme , zda je funkce spojitá
> iscont(f(x),x=-4..4);
![]()
Protože funkce není spojitá na R , určíme body nespojitosti
> discont(f(x),x);
![]()
Výsledek ověříme z grafu funkce
> plot(f(x),x=-4..4,discont=true,
> axesfont=[TIMES,ROMAN,15], labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index57.gif)
> Limit(f(x),x=-1,right)=limit(f(x),x=-1,right);
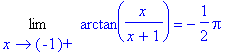
> Limit(f(x),x=-1,right)=limit(f(x),x=-1,right);
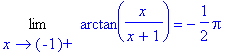
>
2.2.4 Příklad 4.
mws verzeNecht´je zadaná funkce f : y = 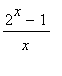 . Vypočteme její limitu v bodě x = 0.
. Vypočteme její limitu v bodě x = 0.
Z definičního oboru funkce vidíme, že x = 0 nepatří do definičního oboru.
Abychom získali představu o průběhu zadané funkce, necháme si vykreslit její graf.
Protože nás zajímá chování funkce v okolí nuly, zobrazíme si graf také podrobněji pro x z intervalu (-0.01..0.01).
f:=x->(2^x-1)/x;
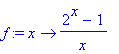
Grafy funkce:
> plot(f(x),x=-10..10,axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index62.gif)
> plot(f(x),x=-0.01..0.01,xtickmarks=3, axesfont=[TIMES, ROMAN, 15], labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index63.gif)
Kromě grafu si můžeme také vypsat tabulku hodnot funkce v okolí nuly.
sez1:=[seq(i, i=2..7)];
![]()
> sez2:=[seq(8-i,i=1..6)];
![]()
> hodn:=[seq(-0.1^i, i=sez1),seq(0.1^i, i=sez2)];
![]()
> seq('f'(i)=evalf(f(i),15), i=hodn);
![]()
![]()
![]()
Z grafu i tabulky můžeme předpokládat , že hodnota limity bude přibližně 0, 6931 .
Přesnou hodnotu určíme :
> with(student,Limit):
> Limit(f(x),x=0):%=value(%);
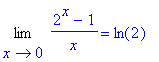
> evalf(ln(2));
![]()
>
2.2.5 Příklad 5.
mws verzeNecht´ g : y = 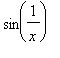 . Co můžete
říci o limitě
. Co můžete
říci o limitě 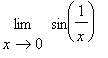 ?
?
Funkci g nadefinujeme, necháme si vykreslit její graf a spočítáme několik funkčních
hodnot v bodech blízkých nule.
g:=x->sin(1/x);
![]()
Graf funkce:
> plot(g(x), x=-1..1, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index75.gif)
Tabulka hodnot:
> 'g'(-0.05)=g(-0.05); 'g'(-0.025)=g(-0.025); 'g'(-0.0025)=g(-0.0025); 'g'(0.0001)=g(0.0001); 'g'(0.0025)=g(0.0025); 'g'(0.001)=g(0.001);
![]()
![]()
![]()
![]()
![]()
![]()
V tomto případě nejde z grafu ani z tabulky hodnotu limity odhadnout. Zkusme tedy určit limitu příkazem Limit .
Výpočet limity:
> with(student,Limit):
> Limit(g(x),x=0);
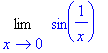
> value(%);
>
![]()
Funkční hodnota pro x->0 leží zřejmě v intervalu <-1,1>. Limita pro x->0 ale neexistuje.
Na předcházejícím obrázku není graf funkce vždy vykreslen až k hodnotám y =-1 a y = 1. Maple vykresluje graf funkce spojováním referenčních bodů. Jejich počet může ovlivnit přesnost grafu. Zvětšíme počet referenčních bodů parametrem numpoints=n . Implicitně je tato hodnota nastavena na n=49.
> plot(g(x), x=-1..1, numpoints=600, axesfont=[TIMES,ROMAN,25],labelfont=[TIMES,ROMAN,25]);
![[Maple Plot]](images/index84.gif)
>
2.2.6 Příklad 6.
mws verzeUrčete hodnotu 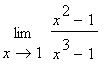
Pro větší názornost nejprve vykreslíme graf funkce
> f:=x-> ((x^2-1)/(x^3-1));
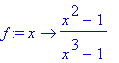
> plot(f(x), x=-5..5, discont=true, axesfont=[TIMES,ROMAN,15],
> labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index87.gif)
Funkce není definována pro x=1, stanovme některé funkční hodnoty v okolí x=1.
> map(t->f(t),[.99,.9999,1.0001,1.1]);
![]()
Definujme novou funkci g splňující podmínku: f(x) = g(x) při D(f) = R-{1}.
Nejdříve rozložíme čitatele a jmenovatele
> factor(numer(f(x)));
> factor(denom(f(x)));
![]()
![]()
Vidíme, že v čitateli i jmenovateli se vyskytuje výraz (x-1), kterým můžeme krátit.
Nová funkce g:
> g := normal(f(x));
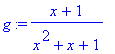
> g:=unapply(g,x);
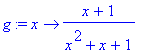
> g(1);
![]()
Funkce g je racionální funkce a je spojitá v bodě 1, což znamená, že její hodnota v tomto bodě je rovna limitě pro x -> 1.
Funkce f a g jsou shodné v okolí bodu x = 1,
můžeme tedy učinit závěr ![]() =
= ![]() =
= ![]() .
.
Výsledek ověříme
> limit(f(x),x=1);
![]()
Výsledek : 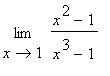 =
= ![]()
>
2.2.7 Příklad 7.
mws verzeMějme funkci h : y = 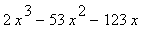 . Jak se h chová pro x ->
. Jak se h chová pro x -> ![]() ?
?
Definujme funkci h:
> h:=x->2*x^3-53*x^2-123*x;
![]()
Graf funkce:
> plot (h(x), x=-10..30, axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index103.gif)
Ilustrační výpočet limity:
> with(student,Limit):
> Limit(vytkni(h(x),x^3), x=infinity);
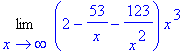
> expand(%);
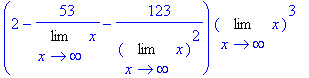
> value(%);
![]()
Ověření hodnoty:
> limit(h(x),x=infinity);
![]()
>
2.2.8 Příklad 8.
mws verzeUrčete limitu 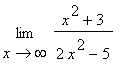
> f:=x->(x^2+3)/(2*x^2-5);
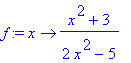
Graf funkce:
> plot(f(x),x=-10.. 10, y=-2..2,axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index110.gif)
> plot(f(x),x=-10.. 10, y=-2..2,axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index111.gif)
Ilustrativní výpočet limity:
> with(student,Limit):
> Limit(vytkni(f(x),x^2), x=infinity);
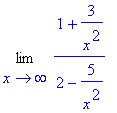
> expand(%);
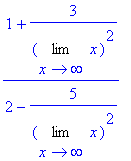
> value(%);
![]()
Ověřeni výsledku:
> limit(f(x), x=infinity);
![]()
>
2.2.9 Příklad 9.
mws verzeUrčete 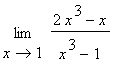 .
.
> f:=x->(2*x^3-x)/(x^3-1);
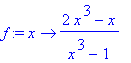
Graf funkce:
> plot(f(x),x=-2..4, y=-10..10,
> labelfont=[TIMES,ROMAN,15],axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index118.gif)
Výpočet limity:
> limit(f(x),x=1);
![]()
Limita tedy neexistuje. Můžeme však určit jednostranné limity.
> limit(f(x),x=1, left);
![]()
> limit(f(x),x=1,right);
![]()
>
3. Definiční obory
Při určování definičních oborů se opíráme o základní znalosti elementárních funkcí.
Příklady:
Určete definiční obory těchto funkcí
a) f(x) = ar ccos
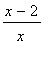
> solve((x-2)/x >=-1 and (x-2)/x <= 1,x);
![]()
podmínka x různé od nuly je také zahrnuta
b) f(x) = ln(sin(x))
budeme zjišťovat, kdy je argument - sin(x) - větší jako 0
> solve(sin(x)>0,x);
vidíme, že MAPLE nám nenabídl žádný výsledek, je tato úloha pro něj neřešitelná
c) f(x) = ln 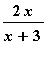
opět řešíme nerovnici, kdy argument je větší než 0, musí platit pro x různé od -3, ve výsledku je také uvažováno
> solve(2*x/(x+3)>0,x);
![]()
d) f(x) = 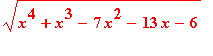
zde víme, že výraz pod sudou odmocninou musí být nezáporný a při "ručním" počítání nejprve rozložíme na kořenové činitele a pak určujeme
znaménko, k rozložení nám poslouží příkaz factor
> factor(x^4+x^3-7*x^2-13*x-6);
![]()
> solve((x+1)^2*(x-3)*(x+2)>=0,x);
![]()
Maple umí ale vyřešit také přímo
> solve(x^4+x^3-7*x^2-13*x-6>=0);
![]()
>
4. Derivace
4.1 Základní informace
Zopakujme některé vlastnosti, které budeme dále využívat.
Existuje-li ![limit((f(x)-f(x[0]))/(x-x[0]),x = x[0])](images/index130.gif) , nazýváme tuto limitu derivace funkce f v bodě
, nazýváme tuto limitu derivace funkce f v bodě ![]() a značíme ji f '(
a značíme ji f '( ![]() ). Obdob ně lze definovat derivaci zprava a
zleva.
). Obdob ně lze definovat derivaci zprava a
zleva.
Z geometrického hlediska představuje derivace funkce v daném bodě směrnici tečny v tomto bodě.
Opakování základních informací o technice derivování
V dalším f,g budou funkce proměnné x .
V každém bodě definičního oboru daných funkcí platí:
(1) (cf)´= cf ´ , c je konstanta
(2) (f + g) ´ = f´+ g´ , platí i pro rozdíl
(3) (f g)´ = f´g + fg´ derivace součinu
(4) ( ![]() )´ =
)´ = 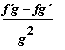 derivace
podílu
derivace
podílu
Připomeneme některé vzorce, které najdeme v každé základní literatuře, pro zajímavost necháme derivace těchto základních funkcí tak, jak
je vypočte MAPLE:
> restart;
> f1:=c: f2:=x^n: f3:=log[a](x): f4:=a^x: f5:=sin(x): f6:=cos(x): f7:=tan(x): f8:=arctan(x): f9:=cot(x): f10:=arccot(x): f11:=arccos(x): f12:=arcsin(x):
> for i from 1 to 12 do
> Diff(f||i,x)=diff(f||i,x)
> od;
![]()
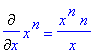
![]()
![]()
![]()
![]()
![]()
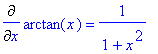
![]()
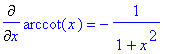
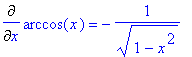
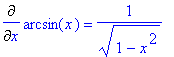
Příkazy systému MAPLE pro derivace
Derivaci můžeme spočítat pomocí příkazu
diff(výraz,proměnná);
kde výraz je algebraický výraz
proměnná je proměnná v tomto výrazu.
Můžeme použít také příkaz Diff( výraz, proměnná); který derivaci nevyhodnotí. Vyhodnocení dosáhneme příkazem value.
4.2 Výpočet derivace
4.2.1 Příklad 1.
mws verzeVypočtěte derivaci funkce f(x) = 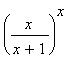 .
.
a) pomocí příkazu diff
> f:=(x/(x+1))^x;
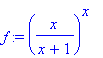
> df:=diff(f,x);
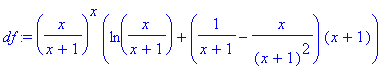
úprava výrazu
> simplify(df,radical);
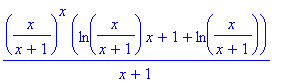
> collect(%,ln(x/(x+1)));
> collect(%,(x/(x+1))^x);
>
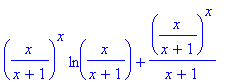
Error, (in collect) cannot collect (x/(x+1))^x
> subs((x/(x+1))^x=t,%%):
> collect(%,t):
> subs(t=(x/(x+1))^x,%);
>
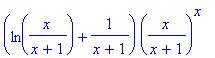
*******************************************************************
b)Výpočet derivace pomocí Diff
> g:=ln((x+1)/(x^2));
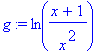
> Diff(g,x);
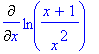
> value(%);
> normal(%);
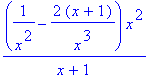
![]()
************************************************************************************
c)Použití operátoru D
> f:=x->(1-ln(x))/(1+ln(x));
![]()
> df:=D(f);
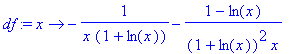
> simplify(df(x));
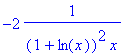
************************************************************************************
4.2.2 Příklad 2.
mws verze> restart;
Vypoctěte první derivaci funkce g(x) = 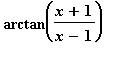
> g:=arctan((x+1)/(x-1));
![]()
> diff(g,x);
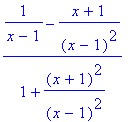
> normal(%);
>
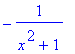
>
4.2.3 Příklad 3.
mws verze> restart;
Vypočtěte první derivaci funkce h(x)
> h:=x->2*ln(2*x-3*(1-4*x^2)^(1/2))-6*arcsin(2*x);
![]()
> dh:=diff(h(x),x);
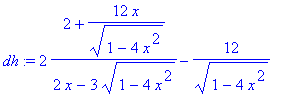
> normal(%);
>
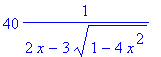
>
4.3 Užití derivací
4.3.1 Tečna
4.3.1.1. Příklad 1.
mws verze> restart;
Pod jakým úhlem se protíná hyperbola h s parabolou p ?.
> h:=1/x; p:=sqrt(x);
![]()
![]()
Průsečík:
> solve(h=p,x);
![]()
Graf křivek a jejich tečen:
> with(student,showtangent):
> with(plots,display):
> plot1:=showtangent(p,x=1,numpoints=600,color=black,labelfont=[TIMES,ROMAN,15]):
> plot2:=showtangent(h,x=1,numpoints=600,color=blue,labelfont=[TIMES,ROMAN,15]):
> display([plot1,plot2],view=[0..4,-1..4],scaling=constrained,
> axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index170.gif)
Směrnice tečen:
> kh:=subs(x=1,diff(h,x));
![]()
> kp:=subs(x=1,diff(p,x));
![]()
Úhel mezi křivkami:
> psi:=arctan(kp);
![]()
> omega:=arctan(kh);
![]()
> delta:=evalf(psi-omega);
![]()
> evalf(convert(delta,degrees));
![]()
úhel křivek je tedy přibližně 72°
>
Ukažme několik ilustrativních příkladů - animací - ukázka grafu a jeho tečny
4.3.1.2 Příklad 2.
> with(plots):
Warning, the name changecoords has been redefined
> f:=x->x^3-5*x^2+x+10;
![]()
> T := (x,a) -> f(a) + (x - a) * D(f)(a) ;
![]()
> display(plot(f(x), x=-2..5,
y=-8..12, color = red),
animate(T(x,t), x=-2..5, t=-1..5, view=-8..12, color = blue, frames=60));
![[Maple Plot]](images/index179.gif)
>
4.3.1.3 Příklad 3.
mws verze> restart;
> with(plots):
Warning, the name changecoords has been redefined
> f:=x->arctan(1/x);
![]()
> T := (x,a) -> f(a) + (x - a) * D(f)(a) ;
![]()
> display(plot(f(x), x=-2..4,
y=-3..3, color = red),
animate(T(x,t), x=-2..3, t=-1..5, view=-3..3, color = blue, frames=60));
![[Maple Plot]](images/index182.gif)
>
4.3.1.4 Příklad 4.
mws verze> restart;
> with(plots):
Warning, the name changecoords has been redefined
> f:=x->exp(1/2*x);
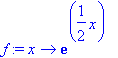
> T := (x,a) -> f(a) + (x - a) * D(f)(a) ;
![]()
> display(plot(f(x), x=-2..5,
y=-8..12, color = red),
animate(T(x,t), x=-2..5, t=-1..5, view=-8..12, color = blue, frames=60));
![[Maple Plot]](images/index185.gif)
>
4.3.2 Průběh funkce
4.3.2.1 Příklad 1.
mws verze> restart;
Vyšetřete průběh funkc e f(x) = 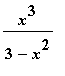 :
:
> f:=x->x^3/(3-x^2);
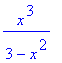
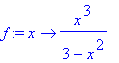
1) Definiční obor:
> solve(denom(f(x))=0,x);
![]()
předcházejícím příkazem jsme nalezli hodnoty, ve kterých funkce není definována,
tedy D(f) = R - {- ![]() }
}
2) Průsečíky s osami:
> {solve(f(x)=0,x)};
![]()
> f(0);
![]()
3) Sudost resp. lichost:
> f(-x);
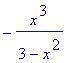
zjistili jsme, že f(-x ) = -f(x), funkce je tedy lichá a graf bude souměrný podle počátku
4) Stacionární body, intervaly monotonie, extrémy
> df:=diff(f(x),x);
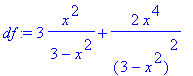
> df:=normal(%);
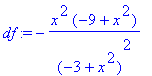
> solve(df,x);
![]()
stacionární body mají tedy souřadnice 0,3,-3 - zjistíme, zda jsou to také extrémy
> solve(df>0,x);
![]()
![]()
> solve(df<0,x);
![]()
ze znaménka první derivace vidíme, že extrémy nastanou v bodech -3,3, dopočítejme souřadnice lokálních extrémů:
> E1:=[-3,f(-3)];E2:=[3,f(3)];
![]()
![]()
5) Intervaly konvexnosti resp. konkavnosti, inflexní body
> dff:=diff(df,x);
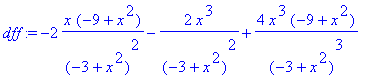
> dff:=normal(%);
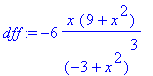
> solve(dff,x);
![]()
> solve(dff>0);
![]()
> solve(dff<0);
![]()
vidíme, že v bodě 0 se mění znaménko 2.derivace, funkce zde má inflexní bod, jeho souřadnice jsou
> Infl:=[0,f(0)];
![]()
6) Asymptoty:
a)se směrnicí y = kx + q
> k1:=limit(f(x)/x,x=-infinity); q1:=limit(f(x)-k1*x,x=-infinity);
![]()
![]()
> k2:=limit(f(x)/x,x=infinity); q2:=limit(f(x)-k2*x,x=infinity);
![]()
![]()
je to přímka y = -x
b)bez směrnice
> Limit(f(x),x=-sqrt(3),left):%=value(%);
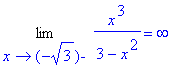
> Limit(f(x),x=-sqrt(3),right):%=value(%);
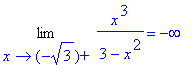
> Limit(f(x),x=sqrt(3),left):%=value(%);
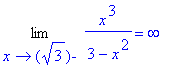
> Limit(f(x),x=sqrt(3),right):%=value(%);
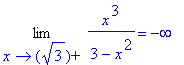
z výpočtu je zřejmé, že funkce má dvě
asymptoty bez směrnice - x = - ![]() , x =
, x = ![]()
7) Graf funkce:
> with(plots,display):
> p1:=plot(f(x),x=-10..10,y=-10..10, discont=true,
> labelfont=[TIMES,ROMAN,15]):
> p2:=plot(-x,x=-10..10,y=-10..10,linestyle=3,
> labelfont=[TIMES,ROMAN,15]):
> p3:=plot([-sqrt(3),t,t=-infinity..infinity],y=-10..10,
> labelfont=[TIMES,ROMAN,15]):
> p4:=plot([sqrt(3),t,t=-infinity..infinity],y=-10..10,
> labelfont=[TIMES,ROMAN,15]):
> display([p1,p2,p3,p4], axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index218.gif)
>
4.3.2.2 Příklad 2.
mws verze> restart;
>
Vyšetřete průběh funkce f( x) = 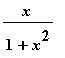
> f:=x->x/(1+x^2);
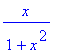
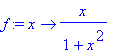
1) určíme definiční obor - funkce je definovaná pro všechna reálná čísla
2) průsečíky s osami
s osou y:
> f(0);
![]()
s osou x:
> solve(f(x)=0);
![]()
3) sudost či lichost
> f(-x);
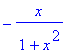
> -f(x);
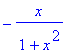
Vidíme, že funkce splňuje podmínku f(-x) = -f(x), je tedy lichá
4) Stacionární body, extrémy, intervaly monotonie
> df:=diff(f(x),x);
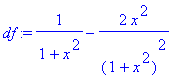
> df:=simplify(df);
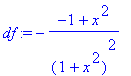
x-ové souřadnice stacionárních bodů
> solve(df);
![]()
nyní zjistíme, jak to vypadá se znaménkem první derivace
> solve(df>0);
![]()
> solve(df<0);
![]()
ve stacionárních bodech se mění znaménko první derivace, jsou to tedy extrémy; souřadnice lokálních extrémů:
> S1:=[-1,f(-1)];S2:=[1,f(1)];
![]()
![]()
podle znaménka vidíme, že bod S1 je lokální minimum, bod S2 lokální maximum
5) případné inflexní body, intervaly, kde je funkce konvexní resp. konkávní
> ddf:=diff(df,x);
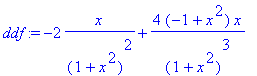
> ddf:=simplify(ddf);
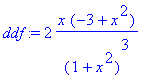
> solve(ddf);
![]()
zjistíme, kde je funkce nad tečnou (tj. konvexní)
> solve(ddf>0);
![]()
a nyní pod tečnou (tj. konkávní)
> solve(ddf<0);
![]()
znaménko druhé derivace se v nalezených bodech mění, jsou to tedy inflexní body
souřadnice inflexních bodů
> I1:=[-sqrt(3),f(-sqrt(3))];I2:=[0,f(0)];I3:=[sqrt(3),f(sqrt(3))];
![]()
![]()
![]()
6) asymptoty funkce
a) se směrnicí
> k1:=limit(f(x)/x,x=infinity); q1:=limit(f(x)-k1*x,x=infinity);
![]()
![]()
> k2:=limit(f(x)/x,x=-infinity); q2:=limit(f(x)-k2*x,x=-infinity);
![]()
![]()
asymptota se směrnicí je přímka y = 0
b) bez směrnice
tyto asymptoty zde neexistují, protože funkce je definovaná na celém R
7) graf funkce:
> plot(f(x),x=-5..5,axesfont=[TIMES,ROMAN,15],labelfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index245.gif)
>
4.3.2.3 Příklad 3.
mws verze> restart;
>
Vyšetřete průběh funkce g(x) = 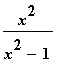
>
> g:=x->x^2/(x^2-1);
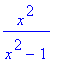
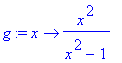
1)Definiční obor funkce - jedná se o racionální funkci, je tedy nutné, aby jmenovatel byl různý od nuly.
> solve(denom(g(x))=0);
![]()
Definiční obor jsou všechna reálná čísla bez {-1,1}
2)Průsečíky s osami:
a) s osou x
> solve(g(x)=0,x);
![]()
>
kořen 0 je dvojnásobný
b) s osou y
> g(0);
![]()
3)Sudost resp. lichost funkce:
> g(-x);
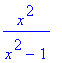
> g(x);
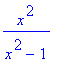
platí g(-x) = g(x) fce je tedy sudá
4)Nalezení stacionárních bodů, intervaly monotonie, případně extrémy
> dg:=diff(g(x),x);
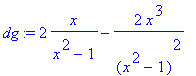
> dg:=simplify(%);
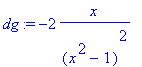
> solve(dg);
![]()
intervaly, kde je funkce rostoucí
> solve(dg>0);
![]()
intervaly, kde je funkce klesající
> solve(dg<0);
![]()
v bodě x = 0 se mění znaménko 1. derivace, funkce zde má extrém, podle znaménka se jedná o lokální maximum
souřadnice stacionárního bodu - lokálního minima
> S:=[0,g(0)];
![]()
5)Intervaly konvexnosti a konkávnosti, případně inflexní body
> ddg:=diff(dg,x);
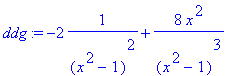
> ddg:=simplify(ddg);
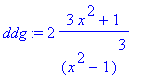
> solve(ddg);
![]()
druhá derivace nemá řešení v oboru reálných čísel, nejsou inflexní body, určíme, kde je funkce nad tečnou a pod tečnou
> solve(ddg>0);
![]()
fce je zde nad tečnou
> solve(ddg<0);
![]()
fce je zde pod tečnou
6)Asymptoty funkce
a) se směrnicí
>
> k1:=limit(g(x)/x,x=infinity); q1:=limit(g(x)-k1*x,x=infinity);
> k2:=limit(g(x)/x,x=-infinity); q2:=limit(g(x)-k2*x,x=-infinity);
![]()
![]()
![]()
![]()
asymptota se směrnicí je tedy přímka y = 1
b) bez směrnice
funkce je nespojitá v bodech -1,1, vypočtěme tedy limity v jejich okolí
> limit (g(x),x=-1);
![]()
limita zde není definovaná, zkusíme limity zprava a zleva
> limit(g(x),x=-1,left);
![]()
> limit(g(x),x=-1,right);
![]()
přímka x = -1 je asymptota bez směrnice a protože daná funkce je sudá, lze říci, že přímka x = 1 je také asymptota bez směrnice
Graf funkce:
> with(plots,display):
> p1:=plot(g(x),x=-5..5,y=-3..5,discont=true,
> labelfont=[TIMES,ROMAN,15]):
> p2:=plot(1,x=-5..5,y=-3..5,linestyle=3,
> labelfont=[TIMES,ROMAN,15]):
> p3:=plot([-1,t,t=-infinity..infinity],x=-5..5,y=-3..5,linestyle=3,
> labelfont=[TIMES,ROMAN,15]):
> p4:=plot([1,t,t=-infinity..infinity],x=-5..5,y=-3..5,linestyle=3,
> labelfont=[TIMES,ROMAN,15]):
> display([p1,p2,p3,p4], axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index272.gif)
>
4.3.2.4 Příklad 4
Vyšetřete průběh funkce h
> h:=x->x^2-4*abs(x)+3;
![]()
>
Definiční obor jsou všechna reálná čísla
Průsečíky s osami:
> solve(h(x)=0,x);
![]()
> h(0);
![]()
Sudá,lichá
> h(-x);
![]()
h(x) = h(-x), funkce je tedy sudá, budeme se pro jednoduchost zabývat průběhem této funkce pro kladné x, protože graf celé funkce je pak souměrný
podle osy y, definujme tuto část dané funkce
> h1:=x->x^2-4*x+3;
![]()
jenom pro doplnění - funkce pro záporné x má
vyjádření h2 = ![]() + 4x + 3
+ 4x + 3
Stacionární body, intervaly monotonie, extrémy
> dh:=diff(h1(x),x);
![]()
> solve(dh=0);
![]()
> solve(dh>0,x);
![]()
> solve(dh<0,x);
![]()
>
Nalezli jsme bod x = 2 jako lokální minimum, protože je funkce sudá, bude bod x = -2 také lokální minimum a musíme se dále zabývat bodem x = 0, kde je funkce definována, ale derivace není - zleva a zprava je různá. V tomto bodě se mění znaménko derivace, nastává zde také extrém - viz další příkazy.
> derivace:=diff(h(x),x);
![]()
> signum(derivace);
![]()
> eval(subs(x=0.5,%));
![]()
derivace je záporná, funkce klesá
> eval(subs(x=-0.5,%%));
![]()
derivace je kladná, funkce roste
> E1:=[-2,h(-2)];E2:=[0,h(0)];E3:=[2,h(2)];
![]()
![]()
![]()
Intervaly, kde je funkce konvexní, resp. konkávní - určujeme pomocí znaménka druhé derivace
> dhh:=diff(dh,x);
![]()
Hodnota druhé derivace je rovna 2, kladného znaménka, z toho tedy vyplývá, že funkce je nad tečnou v celém svém definičním oboru.
Asymptoty:
> k:=limit(h1(x)/x,x=infinity); q:=limit(h1(x)-k*x,x=infinity);
![]()
![]()
Neexistují žádné asymptoty
Graf funkce:
> plot(h(x),x=-5..5,y=-5..5,labelfont=[TIMES,ROMAN,15],
> axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index293.gif)
>
4.3.2.5 Příklad 5.
mws verze> restart;
>
Znázorněte graf funkce f (x) = 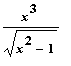
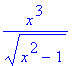
> f:=x->x^3/(x^2-1)^(1/2);
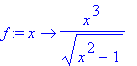
Definiční obor, průsečíky s osami:
> solve(x^2-1>0,x);
![]()
> prusecik:=solve(f(x),x);
![]()
> f(-x):=f(-x);
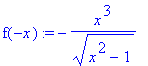
Platí, f(-x) = - f(x), funkce je tedy lichá.
Určíme první derivaci a případné extrémy:
> df:=diff(f(x),x);
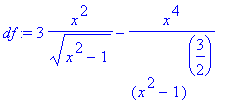
> df:=factor(df);
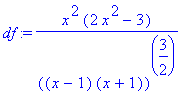
> e:=solve(df,x);
![]()
> solve(df>0);
![]()
> solve(df<0);
![]()
Uvědomíme si, že bod x = 0 nepatří do definičního oboru, extrémy funkce tedy jsou:
> E1:=simplify([e[3],f(e[3])]);E2:=simplify([e[4],f(e[4])]);
![]()
![]()
Nyní vypočteme druhou derivaci a zjistíme, zda existují inflexní body:
> dff:=diff(df,x);
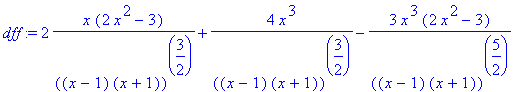
> dff:=factor(dff);
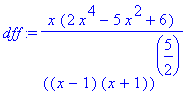
> solve(dff,x);
![]()
Při hledání inflexních bodů zjišťujeme, že jediný reálný bod leží mimo definiční obor. Zaměříme se tedy pouze na konvexitu a konkavitu.
> solve(dff>0,x);
![]()
> solve(dff<0,x);
![]()
Asymptoty
a) se směrnicí
> k1:=limit(f(x)/x,x=infinity);k2:=limit(f(x)/x,x=-infinity);
![]()
![]()
neexistují asymptoty se směrnicí
b) bez směrnice
> limit(f(x),x=-1,left);limit(f(x),x=1,right);
![]()
![]()
funkce má asymptotu bez směrnice x = -1 zleva a x = 1 zprava
Graf funkce:
> p1:=plot(f(x),x=-5..5, y=-5..5,discont=true,
> labelfont=[TIMES,ROMAN,15]):
> p2:=plot([-1,t,t=-infinity..infinity],x=-5..5,y=-5..5,linestyle=3,
> labelfont=[TIMES,ROMAN,15]):
> p3:=plot([1,t,t=-infinity..infinity],x=-5..5,y=-5..5,linestyle=3,
> labelfont=[TIMES,ROMAN,15]):
> with(plots,display):
> display({p1,p2,p3},axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index316.gif)
>
4.3.2.6 Příklad 6.
mws verze> restart;
>
Vyšetřete průběh funkce f(x) = 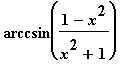
>
> f:=x->arcsin((1-x^2)/(1+x^2));
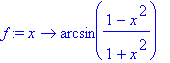
Definiční obor funkce:
> solve(((1-x^2)/(1+x^2))>=-1 and (1-x^2)/(1+x^2)<=1,x);
![]()
- jsou to všechna reálná čísla
Průsečíky s osami:
> solve(f(x)=0);
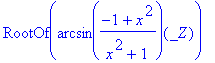
> f(0);
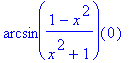
Sudost resp. lichost funkce:
> f(-x):=f(-x);
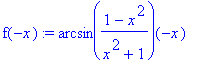
funkce je sudá
Stacionární body, intervaly monotonie; extrémy
> df:=diff(f(x),x);
![]()
> df:=normal(%);
![]()
Upravíme tuto derivaci s ohledem na hodnotu proměnné x
a) x > 0
> assume(x>0):df:=diff(f(x),x);df:=normal(%);
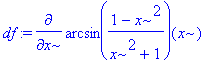
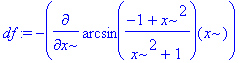
b) x < 0
> assume(x<0):df:=diff(f(x),x);df:=normal(%);
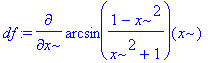
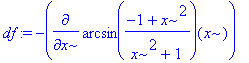
> solve(df);
Error, (in solve) cannot solve expressions with diff(arcsin((-1+x^2)/(x^2+1))(x),x) for x
Neexistuje nulový bod 1. derivace, v bodě x = 0 se však mění její znaménko, nastává tedy extrém - lokální maximum.
Intervaly konvexnosti resp. konkávnosti, inflexní body.
> dff:=diff(df,x);
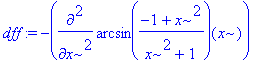
Vypočtená derivace platí pro x < 0 , bylo takto naposledy přiřazeno příkazem assume, její znaménko je tedy kladné, funkce je v tomto
intervalu nad tečnou. Totéž platí pro kladné x, protože se jedná o funkci sudou.
Asymptoty:
a) bez směrnice neexistují - fce je definována na R.
b) se směrnicí
> k:=limit(f(x)/x,x=-infinity); q:=limit(f(x)-k*x,x=-infinity);
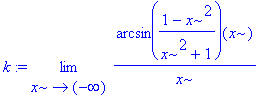
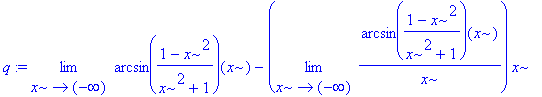
je to tedy pří mka y
= - ![]()
![]()
Graf funkce:
> with(plots,display):
> p1:=plot(-Pi/2,x=-10..10,linestyle=3,labelfont=[TIMES,ROMAN,15]):
> p2:=plot(f(x),x=-10..10,labelfont=[TIMES,ROMAN,15]):
> display({p1,p2},axesfont=[TIMES,ROMAN,15]);
![[Maple Plot]](images/index334.gif)
>
4.3.2.7 Příklad 7.
mws verzeV tomto příkladě je ukázka naprogramované procedury, která určí geometrický význam 1. a 2. derivace funkce.
> restart;
> changes:=proc(f::anything,n::nonnegint)
> local sing,a,i,s,nezn,j,k,vyr,mn,m;
> sing:=[singular(f)];
> a:={};
> m:={};
> for i from 1 to nops(sing) do
> nezn:=indets(op(2,op(1,op(i,sing))));
> if nops(nezn) = 0 then
> if abs(op(2,op(1,op(i,sing)))) < infinity then
> a:=a union op(i,sing);
> m:=m union {op(2,op(1,op(i,sing)))};
> end if;
> else
> for j from 1 to n do
> mn:={};
> for k from 1 to nops(nezn) do
> mn:=mn union {nezn[k]=j};
> end do;
> vyr:=evalf(subs(mn,op(i,sing)));
> a:=a union vyr;
> m:=m union {op(2,op(1,vyr))};
> end do;
> end if;
> end do;
> for i from 1 to n do
> vyr:=fsolve(f,x=i,avoid=a,maxsols=1,-100..100);
> if type(vyr,'float') then
> a:=a union {x=vyr};
> else
> return [a,m];
> end if;
> end do;
> return [a,m];
> end proc:
>
> prubeh:=proc(f::anything,n::nonnegint)
> local g,h,l,s,a,p,q,m,r;
> g:=diff(f(x),x);
> r:=changes(g,n);
> a:=r[1];m:=r[2];
> s:=sort([seq(op(2,op(i,a)),i=1..nops(a))],`<`);
> if nops(s) = 0 then
> if subs(x=0,g)>0 then
> printf("Rostouci na definicnim oboru");
> else
> printf("Klesajici na definicnim oboru");
> end if;
> else
> p:=evalf(subs(x=s[1]-1,g));
> if p>0 then
> printf("Rostouci do bodu %f\n",s[1]);
> else
> printf("Klesajici do bodu %f\n",s[1]);
> end if;
> for l from 1 to nops(s)-1 do
> q:=evalf(subs(x=(s[l]+s[l+1])/2,g));
> if p*q < 0 and nops({s[l]} intersect m) = 0 then
> if p>0 then
> printf("Lokalni maximum v bode %f\n",s[l]);
> else
> printf("Lokalni minimum v bode %f\n",s[l]);
> end if;
> end if;
> if q>0 then
> printf("Rostouci na intervalu (%f, %f)\n",s[l],s[l+1]);
> else
> printf("Klesajici na intervalu (%f, %f)\n",s[l],s[l+1]);
> end if;
> p:=q;
> end do;
> q:=evalf(subs(x=s[nops(s)]+1,g));
> if p*q < 0 and nops({s[nops(s)]} intersect m) = 0 then
> if p>0 then
> printf("Lokalni maximum v bode %f\n",s[nops(s)]);
> else
> printf("Lokalni minimum v bode %f\n",s[nops(s)]);
> end if;
> end if;
> if q>0 then
> printf("Rostouci od bodu %f\n",s[nops(s)]);
> else
> printf("Klesajici od bodu %f\n",s[nops(s)]);
> end if;
> end if;
> h:=diff(g,x);
> r:=changes(h,n);
> a:=r[1];m:=r[2];
> s:=sort([seq(op(2,op(i,a)),i=1..nops(a))],`<`);
> if nops(s) = 0 then
> if subs(x=0,h)>0 then
> printf("Konvexni na definicnim oboru");
> else
> printf("Konkavni na definicnim oboru");
> end if;
> else
> p:=evalf(subs(x=s[1]-1,h));
> if p>0 then
> printf("Konvexni do bodu %f\n",s[1]);
> else
> printf("Konkavni do bodu %f\n",s[1]);
> end if;
> for l from 1 to nops(s)-1 do
> q:=evalf(subs(x=(s[l]+s[l+1])/2,h));
> if p*q < 0 and nops({s[l]} intersect m) = 0 then
> printf("Inflexe v bode %f\n",s[l]);
> end if;
> if q>0 then
> printf("Konvexni na intervalu (%f, %f)\n",s[l],s[l+1]);
> else
> printf("Konkavni na intervalu (%f, %f)\n",s[l],s[l+1]);
> end if;
> p:=q;
> end do;
> q:=evalf(subs(x=s[nops(s)]+1,h));
> if p*q < 0 and nops({s[nops(s)]} intersect m) = 0 then
> printf("Inflexe v bode %f\n",s[nops(s)]);
> end if;
> if q>0 then
> printf("Konvexni od bodu %f\n",s[nops(s)]);
> else
> printf("Konkavni od bodu %f\n",s[nops(s)]);
> end if;
> end if;
> end proc:
Využití procedury pro informace o dané funkci, pro kontrolu je nakreslen graf
a) f(x) = ![]()
> prubeh(x->1/x,4);plot(1/x,x=-2..2,y=-10..10);
Klesajici do bodu 0.000000
Klesajici od bodu 0.000000
Konkavni do bodu 0.000000
Konvexni od bodu 0.000000
![[Maple Plot]](images/index336.gif)
b) f(x) = ![]()
> prubeh(x->x^2,4);plot(x^2,x=-10..10);
Klesajici do bodu 0.000000
Lokalni minimum v bode 0.000000
Rostouci od bodu 0.000000
Konvexni na definicnim oboru
![[Maple Plot]](images/index338.gif)
c) f(x) = x ![]()
> prubeh(x->x*exp(x),10);plot(x*exp(x),x=-10..10,y=-1..10);
Klesajici do bodu -1.000000
Lokalni minimum v bode -1.000000
Rostouci od bodu -1.000000
Konkavni do bodu -2.000000
Inflexe v bode -2.000000
Konvexni od bodu -2.000000
![[Maple Plot]](images/index340.gif)
d) f(x) = xln(x)
> prubeh(x->x*ln(x),10);plot(x*ln(x),x=0..10,y=-10..10);
Klesajici do bodu 0.000000
Klesajici na intervalu (0.000000, .367879)
Lokalni minimum v bode .367879
Rostouci od bodu .367879
Konkavni do bodu 0.000000
Konvexni od bodu 0.000000
![[Maple Plot]](images/index341.gif)
V uvedených příkladech je nutné uvažovat definiční obor, procedura se tímto problémem nezabývá.
>
4.3.3 Taylorův rozvoj
Taylorův polynom funkce je důležitá součást diferenciálního počtu. Ukažme na několika příkladech, jak se tento rozvoj počítá pomocí Maple
Příkaz, který použijeme, má tuto strukturu:
taylor ( výraz, rov/jm, n);
kde výraz je rozvíjená funkce
rov/jm je rovnice tvaru x = a nebo jméno proměnné
n je celočíselná kladná konstanta
4.3.3.1 Příklad 1.
Najděte Taylorův polynom pro tyto funkce:
a) arcs in
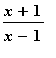 v okolí počátku, stupeň 3
v okolí počátku, stupeň 3
> taylor(arcsin((x+1)/(x-1)),x=0,3);
Error, does not have a taylor expansion, try series()
Vidíme, že Taylorův polynom zde nelze najít - pravé okolí bodu x = 0 totiž nepatří do definičního oboru:
> solve((x+1)/(x-1)>=-1 and (x+1)/(x-1)<=1,x);
![]()
Vybereme x = -1, který patří do definičního oboru:
> taylor(arcsin((x+1)/(x-1)),x=-1,3);
![]()
>
b) cos(x) v okolí počátku, stupeň 6
> taylor(cos(x),x,6);
![]()
c) ![]() , p ro x = 0 a x = 1, stupeň 4
, p ro x = 0 a x = 1, stupeň 4
> taylor(exp(x),x,4);
![]()
> taylor(exp(x),x=1,4);
![]()
>