Metoda prosté iterace

Při řešení rovnice (1) na intervalu 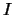iterací se rovnice 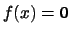převede na ekvivalentní tvar

se zvolí a pro vytvoří iterační posloupnost, jejíž limita je řešením úlohy (1).

Věta 5. Nechť je uzavřený interval a zobrazení s vlastností pro všechna . Pak je kontrakce v úplném metrickém prostoru s koeficientem .

Důkaz. Stačí ověřit, že , tj. pro všechna : Podle Lagrangeovy věty o přírůstku funkce platí

pro vhodný bod mezi . Pak zřejmě a tedy

Důsledek. Jsou-li splněny předpoklady Věty 5, pak pro řešení úlohy (2) platí všechna tvrzení Věty o kontrakci.

Příklad 1. Určete všechny kořeny rovnice s přesností na čtyři desetinná místa.

Grafická metoda:

Schematické znázornění grafu funkcí a na obr. 4 ilustruje skutečnost, že rovnice má právě dva kořeny a

Obrázek 4

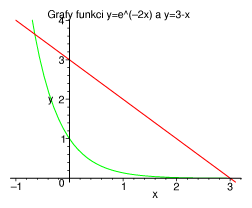
. Za účelem řešení rovnice iterací převedeme původní rovnici na tvar (2).

 a) . Protože

užijeme této ekvivalentní formulace pro aproximaci kořene . Položíme a pro budeme postupně počítat

Viz tabulku níže.

b) . Protože

lze této formulace užít pro aproximaci podle předpisu

Viz tabulku.

Použití metody prosté iterace lze procvičit ve cvičení metoda prosté iterace pro jednu rovnici o jedné neznámé.

   
  Obsah