Předpokládejme, ze aproximace
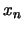 leží blízko kořene
leží blízko kořene
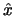 rovnice (1) a
rovnice (1) a 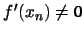 . Pak
. Pak
|
|
|
|
(3) |
|
|
|
|
(4) |
|
|
|
|
(5) |
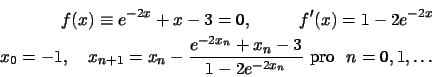
![]()
Next: Iterační metody řešení systémů
Up: Iterační metody řešení jedné
Previous: Metoda prosté iterace
Obsah